wymierna 5-latek : Zapytam się o taka rzecz

	|x−1|
Kiedys pytałem na forum czy funkcja postaci y=		jest funkcja wymierna
	|x|−1

WEdlug mnie jest bo tylko dla x=−1 i x=1 mianownik się zeruje a nie dla każdego x_sa . jednak dostałem tez odpowiedz ze nie jest , Gdyz modul nie jest funkcja wymierna (aktualnie przerabiam ten dzial ) Nie zdazylem dopytać dlaczego gdyż było już pozno w nocy i mnie rozlozylo Pytam w kontekście tego gdyż mam do zrobieni takie cwiczenie Narysuj wykres funkcji

	1		1		1
y=−		y=−		i y=
	x		|x|		|x|

Nie mam problemu z narysowaniem wykresow ale chodzi o to która z tych funkcji jest hiperbola

Janek191:

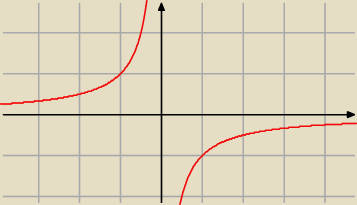
	1
Wykresem funkcji y = −		jest hiperbola.
	x

5-latek : Witaj trochę z rozpedu pisałem to ostatnie cwiczenie A jeśli chodzi o to 1 pytanie ?

Jerzy: Cześć Musisz przeanalizować tą funkcję w czterech przedziałach

5-latek : Janek 191 Chodzi mi tylko o odpowiedz czy to jest funkcja wymierna Mam napisane tak . Funkcja wymierna jest to iloraz wielominow jednej zmniennej , jejdziedzina jest zbior tych x dla których mianownik jest różny od zera Teraz czy wyrażenie postaci |x|−1 jest wielomianem jednej zmniennej ? Jeśli tak to jest to funkcja wymnierna według tej definicji jeśli nie to nie będzie to funkcja wymierna według tej definicji

wredulus_pospolitus: g(x) = |x| nie jest funkcją wymierną, ponieważ nie jest postaci ilorazu funkcji wielomianowych innymi słowy −−− aby funkcja f(x) była funkcją wymierną, musimy mieć iloraz dwóch WIELOMIANÓW, a 'moduł x' nie jest wielomianem

5-latek : dzień dobry czyli jeśli mam np. postac czy w liczniku czy w mianowniku z modulem np. |x|+2 ,czy powiedzmy |x−5| nie będzie to funkcja wymnierna gdyż te postacie nie sa wielomianami ?

5-latek : Jeśli tak to o to chodzilo i dziekuje

Jerzy: Przypadek 1) Dla x < −1 masz fragment hiperboli .. itd.

5-latek : czesc To podobnie funkcja w myśl tego ze modul nie ejst wielomianem

	x
f(x)=		= sgnx tez nie jest funkcja wymierna
	|x|

Jerzy: Definicja f. wymiernej ściśle ją określa i każda f. która nie spełnia warunków, nie jest f.wymirną

5-latek :

	a
CHe to juz skonczyc zeby przejsc do analizy wyktesow postaci fa(x)=		znanymi z
	x

podsatwowki i dopytac Funcje postaci y=1 i y={x}{x} dla x≠0 to sa oczywiscie funkcje wymierne

5-latek :

5-latek :

Mila: tak .

5-latek : dobrze