Równanie stycznych prostopadłych Meszka: Napisz równania stycznych do okręgu o równaniu x2−4x+y2−2x+1 prostopadłych do prostej o równaniu y=−1/2x+5 Proszę o rozwiazanie z wytłumaczeniem

cre: na początek napisz bez błędów równanie okręgu

Meszka: Jak masz z tylu po x 2 to jest do kwadratu. I po y tez

Meszka: X²−4x+y²−2x+1

5-latek : Czyli jak to mowi moja kolezanka Można ? można . A jednak nie można x²−4x+y²−2y+1=0 (x−2)²+(y−1)²= 4 Ten rysunek którego nie chialo CI się zrobić powinien nasunąć CI co najmniej dwa rozwiązania tego zadania .

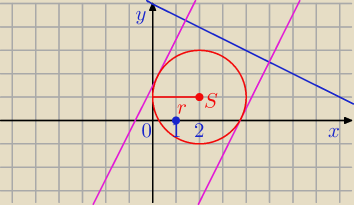
Janek191: x² − 4 x + y² − 2 y + 1 = 0 ? ( x − 2)² − 4 + ( y − 1)² − 1 + 1 = 0 ( x −2)² + ( y − 1)² = 2² S = ( 2, 1) r = 2 oraz

	1
y = −		x + 5
	2

więc proste prostopadłe będą miały równania y = 2 x + b lub 2 x − y + b = 0 Odległość tych prostych od środka okręgu S = ( 2, 1) jest równa r = 2, zatem

I 2*2 −1*1 + b I
	= 2
√22 +(−1)2

I 3 + b I = 2√5 ( 3 + b)² = 4*5 = 20 9 + 6 b + b² − 20 = 0 b² + 6 b − 11 = 0 Δ = 36 − 4*1*(−11) = 36 + 44 = 80 = 16*5 √Δ = 4√5

	− 6 − 4√5
b =		= − 3 − 2√5 lub b = − 3 + 2√5
	2

Równania prostych stycznych: y = 2 x − 3 − 2√5 oraz y = 2 x − 3 + 2√5 ============================================

Janek191: Ten Meszka to leń. Nie chce mu się nawet napisać porządnie równania okręgu i trzeba się go domyślać

Janek191: A x + B y + C = 0 − równanie prostej P = (x₀, y₀) odległość punktu P od prostej danej wyżej obliczamy ze wzoru

	I A*x0 + B*y0 + C I
d =
	√A2 + B2