Bardzo bym prosiła z obiaśnieniem zaczęłam robić ale coś mi nie wychodzi
małgosia: Dany jest trójkąt A(1,2) B (−1,−1) C(5,2) Napisz :
a) równanie wysokości poprowadzonej z wierzchołka C
b) długość taj wysokości
c) pole tego trójkąta
d)współrzędne tego punktu D takiego, aby czworokąt ABCD był równoległobokiem
2 sty 21:46
Anna: pomogę
2 sty 22:04
Anna:
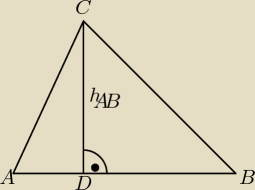
a) h
AB = ? A(1,2), B(−1, −1), C(5,2)
| | yB − yA | | −1−2 | | 3 | |
aAB = |
| = |
| = |
| |
| | xB − xA | | −1−1 | | 2 | |
Równanie wysokości h
AB :
y − y
C = a
CD(x − x
C)
b) I h
ABI = ICDI − obliczymy np. ze wzoru na odległość punktu C od prostej AB.
| | IAxC + ByC + CI | |
d = |
| |
| | √A2+B2 | |
W tym celu należy wyznaczyć równanie ogólne prostej AB.
y − y
A = a
AB(x − x
A)
| | 3 | | 1 | | 3 | | 1 | |
y = |
| x + |
| ⇒ |
| x − y + |
| = 0 /*2 |
| | 2 | | 2 | | 2 | | 2 | |
3x − 2y + 1 = 0
| | I3*5−2*2+1I | | 12 | | 12√13 | |
Czyli: IhABI = |
| = |
| = |
| |
| | √32+(−2)2 | | √13 | | 13 | |
Osobno poślę punkty c) i d).
2 sty 22:30
Anna:
IABI =
√(xB−xA)2 + (yB−yA)2 =
√(−1−1)2 + (−1−2)2 =
√4+9 =
√13
| | 1 | | 12√13 | |
PABC = |
| *√13 * |
| = 6 |
| | 2 | | 13 | |
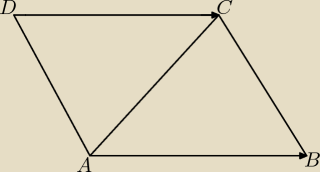
d) Współrzędne wierzchołka D równoległoboku ABCD najprościej można obliczyć z równości
wektorów AB i DC.
−−>
AB = [x
B − x
A, y
B − y
A] = [−1−1, −1−2] = [−2, −3]
−−>
DC = [x
c − x
D, y
C − y
D] = [5 − x
D, 2 − y
D]
−−> −−>
AB = DC ⇔ 5 − x
D = −2 ∧ 2 − y
D = −3
x
D = 7 y
D = 5
Czyli:
D(7, 5)
2 sty 22:50
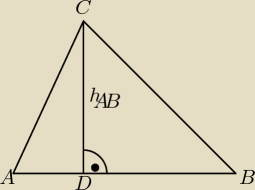 a) hAB = ? A(1,2), B(−1, −1), C(5,2)
a) hAB = ? A(1,2), B(−1, −1), C(5,2)
