Równania zespolone
qazxsw21: mam problem z dwoma równaniami z l.zespolonymi
1) z4 +1 +i = 0
2) z4 − i = 0
jakieś pomysły ?
14 kwi 21:41
piotr: t=z2
14 kwi 21:49
piotr: i delta
14 kwi 21:49
qazxsw21: tak myślalem, ale co dalej z tym zrobić, to i mnie męczy
14 kwi 21:50
Janek191:
1) z4 + 1 + i = 0
z4 = −1 − i
I teraz oblicz 4 pierwiastki z liczby ( − 1 − i )
14 kwi 21:50
qazxsw21: ad1
t2 +1 +i = 0 .... ?
14 kwi 21:50
qazxsw21: Janek tym sposobem też można ?
14 kwi 21:51
Mila:
Wzory de Moivre'a.
14 kwi 21:52
qazxsw21: a propo delty z t2 +1 + i = 0, gdzie jest b a gdzie c ?
14 kwi 21:53
qazxsw21: coś myślę, że z tą deltą to jednaqk nie najlepszy pomysł
14 kwi 21:53
Janek191:
| | ( 1 + i)2 | |
2) z4 = i = (0,5 *2 i) = |
| |
| | 2 | |
| | 1 + i | | √2 | | √2 | |
z2 = |
| = |
| + |
| i itd. |
| | √2 | | 2 | | 2 | |
14 kwi 21:54
qazxsw21: a mogę to zrobić tak ?
z
4 − i= 0
(z
2 −i)(z
2 +i)=0
(z−i)(z+i)(z
2+i)=0 −−−> wtedy z
1 = i i z
2 = −i
a reszta:
z
2 = −i i z tego policzyć pierwiastek, wtedy chyba wyjdzie:
14 kwi 22:17
piotr: źle
14 kwi 22:23
qazxsw21: no to już nie ogarniam
14 kwi 22:27
Mila:

2)
z
4 − i = 0⇔
z
4=i liczba i to na płaszczyźnie punkt(0,1)
z=
4√i
u=i
|u|=|i|=1
| | | | | |
zk=√1*(cos |
| +i sin |
| ) gdzie k∊{0,1,2,3} |
| | 4 | | 4 | |
| | | | | | 5π | | 5π | |
z1=cos |
| +i sin |
| )=cos |
| +i sin |
| |
| | 4 | | 4 | | 8 | | 8 | |
| | | | | | 9π | | 9π | |
z2=cos |
| +i sin |
| )=cos |
| +i sin |
| |
| | 4 | | 4 | | 8 | | 8 | |
| | | | | | 13π | | 13π | |
z3=cos |
| +i sin |
| )=cos |
| +i sin |
| |
| | 4 | | 4 | | 8 | | 8 | |
14 kwi 22:39
Janek191: | | π | |
i to tyle Milu ?  miałem tak robić ale wsytarszyłem się |
| , swierdziłem że znajdę w |
| | 8 | |
tablicach takich ładnych wartości, a tu się okazuje że wynikiem mogą by powiedzmy "brzydkie"
pierwiastki ?

14 kwi 22:46
Janek191: *nie znajdę
14 kwi 22:47
Janek191:
Kto się podszywa pode mnie ?
14 kwi 22:49
Mila:
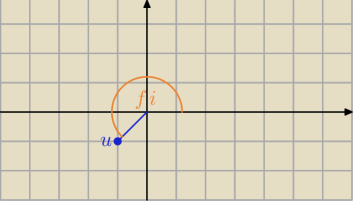
1)
z
4 +1 +i = 0
z
4=−1−i
u=−1−i
|u|=
√12+12=
√2
| | | | | |
zk=4√√2*(cos |
| +i sin |
| ), k∊{0,1,2,3} |
| | 4 | | 4 | |
4√√2=
8√2
Licz tak jak w poprzednim zadaniu pokazałam.
14 kwi 22:51
Mila:
Myślę, że można zostawić w postaci trygonometrycznej.
14 kwi 22:52
qazxsw21: ja przez przypadek, skopiowałem sobie twój nick żeby w razie w wiedzieć kogo pytać o pomoc, ale
przyapdkie mwcisnąłem tab i jak chciałem wkleić to zamieniło mój nick
14 kwi 23:01
 2)
z4 − i = 0⇔
z4=i liczba i to na płaszczyźnie punkt(0,1)
z=4√i
u=i
2)
z4 − i = 0⇔
z4=i liczba i to na płaszczyźnie punkt(0,1)
z=4√i
u=i
 miałem tak robić ale wsytarszyłem się
miałem tak robić ale wsytarszyłem się 
 1)
z4 +1 +i = 0
z4=−1−i
u=−1−i
|u|=√12+12=√2
1)
z4 +1 +i = 0
z4=−1−i
u=−1−i
|u|=√12+12=√2