Oblicz: alexaa: Punkt A(6;−9) jest wierzchołkiem kwadratu. Oblicz pole kwadratu, jeśli jeden z jego boków zawiera się w prostej 4x−3y+9=0

Janek191:

	4
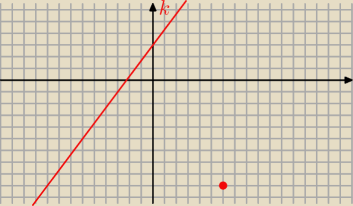
k : 4 x − 3 y + 9 = 0 lub y =		x + 3
	3

A = ( 6, − 9) Obliczam odległość punktu A od prostej k

	I 4*6 − 3*(−9) + 9 I		60
a =		=
	√36 + 81		√117

więc pole kwadratu

	3 600
P = a2 =
	117

=================

Janek191: Pomyłka − zaraz poprawie

Janek191:

	I 4*6 − 3*(−9) + 9 I		60
a =		=		= 12
	√42 + (−3)2		5

Pole kwadratu P = a² = 144 [j²] =============

P: @ Janek ? ?

	60
a=		to P=a2=....
	5