Romb Less: Romb o kącie ostrym α zgięto wzdłuż przekątnej przeciwległej temu kątowi tak, że połówki tego rombu stały się prostopadłe. Wyznacz kosinus kąta β zawartego między bokami tak zagiętego rombu, wychodzącymi z wierzchołka należącego do osi zgięcia. Sporządź odpowiedni rysunek.

Less: Odświeżam, proszę o pomoc.

Less: ⇔

Iryt: Masz odpowiedź?

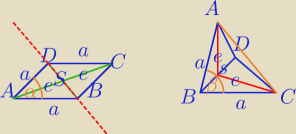
Iryt: |AC|=2e W ΔASB:

	α		e
cos		=
	2		a

	α
e=a*cos
	2

W ΔASC:

	α
|AC|=e√2=a√2cos
	2

W ΔABC z tw. cosinusów: |AC|²=a²+a²−2*a*a*cosβ

	α
2a2*cos2		=2a2−2a2*cosβ /:(2a2)
	2

	α
cos2		=1−cosβ
	2

	α
cosβ=1−cos2
	2

	α
cosβ=sin2
	2

===========

Iryt:

Less:

	1−cosα
Odpowiedź to cosβ=
	2

Iryt: To się zgadza. Przelicz, że:

	1−cosα		α
		=sin2
	2		2

Less: Wiem, że się zgadza. Dzięki za pomoc

Mila: ♠