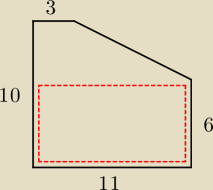
optymalizacja elly: Z kawałka blachy należy wyciąć prostokąt o największym polu, w taki sposób jak zostało to pokazane na rysunku (wierzchołek P prostokąta ma należeć do krawędzi CD). Znajdź wymiary tego prostokąta. Odp. 11x6 http://192.166.218.70/png/rysunek111588.png

Jerzy: Schemat...uzależniasz pole od jednej zmiennej i liczysz maksimum

Jerzy: Wskazówka..od pola całego trapezu odejmujesz pola dwóch mniejszych

Jerzy: Od pola pięciokąta

Jerzy: Jeśli rysunek dobry, to odpowiedż zła

wredulus_pospolitus: Rysunek jest całkowicie skopany. Nawet gdyby przyjąć, że jest poprawny (a odpowiedź błędna), to i tak wychodzą bzdury

elly: rysunek identyczny jak w podreczniku i odp tez jest to zadanie z kiełbasy, wiec wysoce prawdopodobne, ze jest blad w odp

Jerzy: Jest na pewno błąd w odpowiedzi

wredulus_pospolitus: Jerzy −−− nie ma x = 11 ; y = 6 prostokąt ma podstawę pięcioboku i wysokość równą prawemu bokowi

	3
maksimum wychodzi dla y = 5		, ale przecież y≥6 ; stąd y=6 i x=11
	4

jc: Odpowiedź jest prawidłowa. Jeden z wierzchołków leży na prostej x + 2y = 23. Pole prostokąta = xy = y(23 − 2y) = (23/4)² − 2(y−23/4)² 23/4 ≤ 6 ≤ y. Zatem, czym mniejsze y weźmiemy, tym większe będziemy mieć pole. Najlepiej więc wybrać y=6. Wtedy x=11 i pole wynosi 11x6=66.