Szereg geometryczny
x: Dziedzina pewnej funkcji f jest równa przedziałowi (12; 1), natomiast jej wartości
spełniają dla każdego x€(12; 1) następujące równanie
1+f(x)+f2(x)+f3(x)+...=1x3+x
w którym lewa strona jest równa sumie wyrazów pewnego nieskończonego ciągu geometrycznego.
Wyznacz zbiór wszystkich wartości funkcji f.
13 kwi 22:54
Janek191:
| 1 | | 1 | | 1 | |
| = |
| ; I f(x) I < 1, x ∊( |
| , 1) |
| 1 − f(x) | | x3 + x | | 2 | |
1 − f(x) = x
3 + x
f(x) = − x
3 − x + 1
Dokończ

13 kwi 22:59
bolek amator: −1/(x3+x) czy 1/(x3+x) ?
13 kwi 23:00
bolek amator: Aha ok
13 kwi 23:01
Qulka: ZW=(−1 ; 3/8)
13 kwi 23:01
13 kwi 23:01
x: Jakie znaczenie ma dla zadania dziedzina podana w poleceniu?
13 kwi 23:05
Qulka: żeby f(x) było ułamkiem i spełniało założenie o zbieżności ciągu
13 kwi 23:06
bolek amator: Ale chyba żeby napisać pierwsze równanie które napisał Janek191 trzeba najpierw mieć to
założenie, dopiero potem można je napisać
13 kwi 23:09
Qulka: W treści Ci napisali że w tym zakresie spełniają
13 kwi 23:10
Janek191:
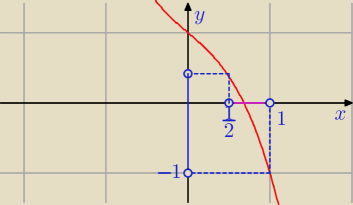
13 kwi 23:11
bolek amator: Ok, no oczywiście, dziękuję
13 kwi 23:12

