Pierwiastki l.zespolonej zespalony: Obliczyć oraz zaznaczyć na płaszczyźnie zespolonej pierwiastki: ⁴√1+i Wiem mniej więcej jak to się liczy, ale wychodzą dość dziwne liczby: |z|=√2, k=0,1,2,3, n=4

	√2		√2		π
cos		, sin		→ φ=
	2		2		4

	π   +0 4		π   +0 4
ω0=4√√2(cos		+isin U		) = −18√2=−8√2
	4		4

reszta będzie ejszcze dziwniejsza.., robię gdzieś błąd ?

zespalony: sorki, wyjdzie wszędzie chyba −8√2 dla 4 pierwiastków, czyli ω₀=ω₁=ω₂=ω₃

zespalony: i jak to mam zaznaczyć na płaszczyźnie zespolonej ? jako jeden pkt ?

zespalony: halo, matematycy ?

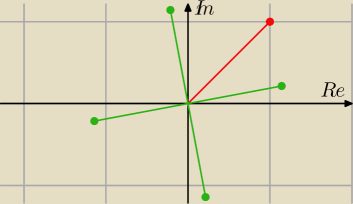
g: Zielone to pierwiastki. Moduł = ⁸√2, kąt = π/16.

zespalony: jsakim cudem moduł jest równy⁸√2 a kąt ^π₁₆ ?

g: ponieważ moduł liczby (1+i) to √2, a kąt π/4. (2^1/2)^1/4 = 2^1/8 = ⁸√2 (π/4)/4 = π/16

zespalony: ajjj, a ja skracałem sobie a powinienem mnożyć przez odwrotność , już kumam