 1. Z punktu P leżącego na zewnątrz koła o środku O i promieniu r poprowadzono do tego okręgu
styczną w punkcie S i prostą przecinającą okrąg w punktach A i B. Wykaż, że |PS|2 = |PA|*|PB|
2. W trójkącie równoramiennym ABC (|AC|=|AB|) środkowe poprowadzone z wierzchołków B i C są
prostopadłe. Wyznacz stosunek długości boków |AC| i |BC|
3. Wykaż, że suma odległości dowolnego punktu należącego do brzegu prostokąta od jego
przekątnych jest wielkością stałą dla danego prostokąta.
1. Z punktu P leżącego na zewnątrz koła o środku O i promieniu r poprowadzono do tego okręgu
styczną w punkcie S i prostą przecinającą okrąg w punktach A i B. Wykaż, że |PS|2 = |PA|*|PB|
2. W trójkącie równoramiennym ABC (|AC|=|AB|) środkowe poprowadzone z wierzchołków B i C są
prostopadłe. Wyznacz stosunek długości boków |AC| i |BC|
3. Wykaż, że suma odległości dowolnego punktu należącego do brzegu prostokąta od jego
przekątnych jest wielkością stałą dla danego prostokąta.


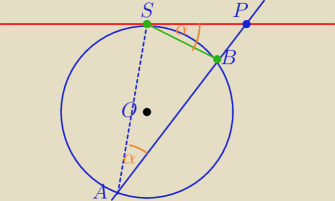 1) Twierdzenie o odcinkach siecznej i stycznej
∡PSB≡∡SAB − kąt między styczną a cięciwą (SB) (tzw. kąt dopisany) jest równy kątowi wpisanemu
opartemu na tej cięciwie (SB)
ΔAPS∼ΔPSB cecha kkk
⇔
1) Twierdzenie o odcinkach siecznej i stycznej
∡PSB≡∡SAB − kąt między styczną a cięciwą (SB) (tzw. kąt dopisany) jest równy kątowi wpisanemu
opartemu na tej cięciwie (SB)
ΔAPS∼ΔPSB cecha kkk
⇔
| |PS| | |PA| | ||
= | ⇔ | ||
| |PB| | |PS| |
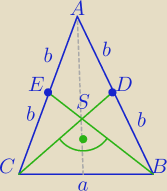 2)
W trójkącie równoramiennym ABC (|AC|=|AB|) środkowe poprowadzone
z wierzchołków B i C są prostopadłe.
Wyznacz stosunek długości boków |AC| i |BC|.
2)
W trójkącie równoramiennym ABC (|AC|=|AB|) środkowe poprowadzone
z wierzchołków B i C są prostopadłe.
Wyznacz stosunek długości boków |AC| i |BC|.
| AC | 2b | ||
= | =? | ||
| BC | a |
| 2 | ||
|CS|=|SB|= | s | |
| 3 |
| 2 | 2 | |||
a2=( | s)2+( | s)2 | ||
| 3 | 3 |
| 4 | 4 | 8 | ||||
a2= | s2+ | s2= | s2 | |||
| 9 | 9 | 9 |
| 2√2 | ||
a= | s | |
| 3 |
| 1 | 2 | |||
|CE|=b, |ES|= | s, |CS|= | s | ||
| 3 | 3 |
| 1 | 2 | |||
b2=( | s)2+( | s)2 | ||
| 3 | 3 |
| 1 | 4 | 5 | ||||
b2= | s2+ | s2= | s2 | |||
| 9 | 9 | 9 |
| √5 | ||
b= | s | |
| 3 |
| 2*b |
| √5 | √10 | |||||||||||||
= | = | = | ⇔ | |||||||||||||
| a |
| √2 | 2 |
| |AC| | √10 | ||
= | |||
| |BC| | 2 |
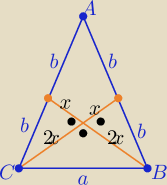 zad 2/
Środkowe dzielą się w stosunku 2:1 licząc od wierzchołka
i w trójkącie równoramiennym są równej długości
skoro z treści zadania są prostopadłe
to z tw. Pitagorasa :
b2=4x2+x2 ⇒ b= √5x i a2=4x2+4x2 ⇒ a= 2√2x
zad 2/
Środkowe dzielą się w stosunku 2:1 licząc od wierzchołka
i w trójkącie równoramiennym są równej długości
skoro z treści zadania są prostopadłe
to z tw. Pitagorasa :
b2=4x2+x2 ⇒ b= √5x i a2=4x2+4x2 ⇒ a= 2√2x
| 2b | 2√5x | √2 | √10 | |||||
zatem: | = | = | = | |||||
| a | 2√2x | √5 | 2 |

| 2√5 | √10 | |||
Literówka  .... = .... = | = | |||
| 2√2 | 2 |




 dla Ety.
Nie chciałam Ci dokuczyć i cieszę się ,że jesteś , zawsze jestem wdzięczna I Tobie i Jankowi,
gdy zwrócicie mi uwagę na niedokładność albo pomyłkę.
Odchodzimy od komputera albo telefon zadzwoni i wtedy coś się sknoci.
Ja zawsze słucham muzyki.
Dla Ety i Janka
https://www.youtube.com/watch?v=YrLTBJj26gs
dla Ety.
Nie chciałam Ci dokuczyć i cieszę się ,że jesteś , zawsze jestem wdzięczna I Tobie i Jankowi,
gdy zwrócicie mi uwagę na niedokładność albo pomyłkę.
Odchodzimy od komputera albo telefon zadzwoni i wtedy coś się sknoci.
Ja zawsze słucham muzyki.
Dla Ety i Janka
https://www.youtube.com/watch?v=YrLTBJj26gs



 moja Anielciu
moja Anielciu 

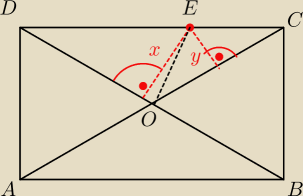 3 zadanko jest 'prozaicznie proste'
Należy zauważyć, że:
3 zadanko jest 'prozaicznie proste'
Należy zauważyć, że:
| x*|DO| | y*|CO| | |||
Pola ΔDOE i ΔOCE można wyznaczyć z: | ; | |||
| 2 | 2 |
