Rówanie okręgu Paweł: Napisz równanie okręgu √5, jeśli punkty A i B należą do tego okręgu A(1,3) B(4,2)

Janek191: Napisz porządnie treść zadania. Czy r = √5 ?

Paweł: Środek okręgu oznaczyłem jako punkt S(x,y) Napisałem układ równań 5=(x−1)² + (y−3)² 5=(x−4)² + (y−2)² Po rozwiązaniu tego układu wyszło mi, że y=3x−5. Czy do tej pory wszystko jest okey?

Paweł: równanie okręgu o promieniu √5

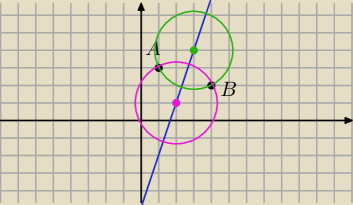
Qulka: tak Twoja prosta jest OK ..to ta niebieska linia

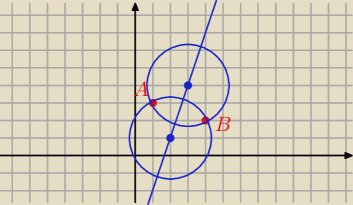
Janek191: Na tej prostej leży punkt S = ( x, 3 x − 5) − środek okręgu

Tadeusz: (x−x_s)²+(y−y_s)²=5

Paweł: Teraz żeby wyliczyć współrzędne środka czyli punktu S to podstawiam: S(x,y)=(x,3x−5) czyli (x−1)²+(3x−8)⁼5 x²−5x−6=0 x1=6 x2=1 Czy to jest dobrze?

Janek191: I AS I² = 5

Tadeusz: Ty szukasz x_s i y_s ... a podstawiasz za x i y

Paweł: Właśnie chodzi o to, że nie wiem jak wyliczyć współrzędne punktu S, chyba, że w obliczeniach robię gdzieś błąd. :<

Qulka: jak widać na obrazku nie jest bo iksy nie pasują ... a czy podniosłeś drugi nawias do kwadratu?

Qulka: Tadeusz..akurat w tym zadaniu nie ma znaczenia czy podstawia za a czy za iks..kwestia nazewnictwa

Janek191: A = (1, 3) S = ( x, 3 x − 5) więc I AS I² = ( x −1)² + ( 3 x − 8)² = 5 x² − 2 x + 1 + 9 x² − 48 x + 64 = 5 10 x² − 50 x + 60 = 0 / : 10 x² − 5 x + 6 = 0 ( x − 2)*( x −3) = 0 x = 2 lub x = 3 ============= Wylicz y −ki

Qulka: jedyny błąd to że przed 6 ma być plus w tym równaniu kwadratowym

Paweł: Podnosiłem. Właśnie widzę, że nie zgadza się z rysunkiem, zresztą z odpowiedzią też. Już wiem gdzie tkwił problem... x²−5x+6=0 a nie x²−5x−6=0

Paweł: Wszystko jasne, dzięki za pomoc

Tadeusz: nie masz racji Qulka .. to błąd

Qulka: przy podnoszeniu do kwadratu tak jak i w module odejmowanie jest przemienne ... również odległość między dwoma puntami nie definiuje, który punkt jest początkiem, a który końcem więc spokojnie można podstawiać w obie strony bo to po prostu odległość dwóch punktów SA i SB albo AS i BS jak wolisz