asd Benny: 1.

	√2+1
Liczba		−√2 jest liczbą:
	√2−1

√2+1		√2+1		√2+1		2+2√2+1
	−√2=		*		−√2=		−√2=
√2−1		√2−1		√2+1		2−1

=3+2√2−√2=3−√2 Jest to liczba niewymierna. 2. Wskaż nierówność, która opisuje sumę przedziałów (−∞; −2> ∪ <4;+∞): |x−1|≥3 x−1≥3 lub x−1≤−3 x≥4 lub x≤−2 x∊(−∞; −2> ∪ <4;+∞) odp. B 3. Liczba log₄32−log₄2 jest równa: log₄32−log₄2=x

	32
log432−log42=log4		=log416
	2

log₄16=x 4^x=16 4^x=4² x=2 4. Narty kosztowały 680zł. O ile procent należałoby obniżyć cenę nart, aby kosztowały 595zł? 100% − 680zł x% − 595zł x*680=59500

	59500
x=
	680

x=87,5% Należy obniżyć o 12,5%. 5.

	−7
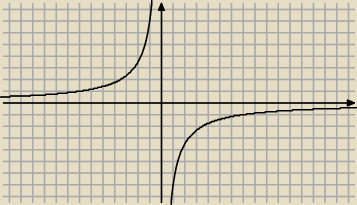
Wykres funkcji f(x)=		znajduje się w ćwiartkach
	x

rys. do zadania Z rysunku widać, że jest to druga i czwarta ćwiartka.

	a
Funkcja hiperboliczna f(x)=		dla a>0 jest w 1 i 3 ćwiartce, a dla a<0 2 i 4 ćwiartka.
	x

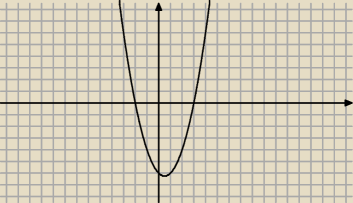
Benny: 6. Funkcje f(x)=−3x+2 i g(x)=2x+7 przyjmują równą wartość dla x równego: f(x)=g(x) −3x+2=2x+7 5x=−5 x=−1 7. Wierzchołek paraboli o równaniu y=−2(x+2)²+4 ma współrzędne równanie paraboli w postaci kanonicznej: y=a(x−p)²+q, gdzie (p, q) to współrzędne wierzchołka, więc współrzędne wierzchołka to (−2; 4) 8. Zbiorem rozwiązań nierówności (x+2)(x−3)≥0 jest: Jest to parabola z ramionami do góry o miejscach zerowych −2 oraz 3, wartości funkcji są nieujemne w przedziale x∊(−∞; −2> ∪ <3;+∞) (rysunek) 9. Wskaż m dla którego funkcja liniowa f(x)=(m+3)x−2 jest malejąca Funkcja liniowa jest malejąca dla a<0 m+3<0 m<−3 m=−4 spełnia nierówność 10. Który z podanych ciągów jest ciągiem geometrycznym? (2, 6, 18) ponieważ kolejne wyrazy są trzy razy większe od poprzednich a₁=2, q=3

Mila: Benny dla kogo te zadania?

Benny: 11. Dla n=1, 2, 3, .... ciąg (a_n) jest określony wzorem a_n=(−1)ⁿ*(3−n). Wtedy a₄: a₄=(−1)⁴(3−4) a₄=−1 a₄<0 12. W ciągu arytmetycznym piąty wyraz jest równy 11, a dziewiąty jest równy 25. Różnica tego ciągu jest równa: a₉=a₁+8r a₅=a₁+4r a₉−a₅=4r 25−11=14 4r=14

	7
r=
	2

13.

	2
Kąt α jest ostry i cosα=		. Wartość wyrażenia 1+sin2α jest równa:
	3

	2
cosα=		/()2
	3

	4
cos2α=
	9

cos²α=1−sin²α

4
	=1−sin2α
9

	5
sin2α=		/+1
	9

	14
sin2α+1=
	9

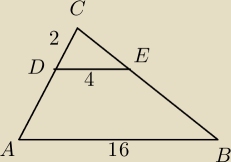
14. Odcinki AB i DE są równoległe. Długości odcinków CD, DE i AB są odpowiednio równe 2, 4, 16. Długość odcinka AD jest równa: Trójkąty ABC i DEC są podobne.

DE		DC
	=
AB		AD+DC

4		2
	=
16		AD+2

1		2
	=
4		AD+2

8=AD+2 AD=6 15. Środek okręgu o równaniu x²+y²−6x+4y+9=0 Równanie okręgu x²+ax+y²+by+c=0

	−a		−b
Środek okręgu (x0, y0) to (		,		), więc w tym wypadku a=−6, b=4
	2		2

środek okręgu (3, −2)

Benny: Milu dla siostry

Mila: A czyta? Nie widzę, aby rozwiązywała.

Benny: 16. Wyniki konkursu podano w punktach: 82, 94, 88, 92, 90, 86, 76, 72. Medianą tego zestawu wyników jest: Trzeba uporządkować rosnąco od najmniejszej: 72, 76, 82, 86, 88, 90, 92, 94 Ilość wyrazów jest parzysta, wiec trzeba wziąć średnią arytmetyczną czwartego i piątego wyrazu:

86+88
	=87
2

17. Objętość sześcianu jest równa 64cm³. Jaka jest suma długości wszystkich krawędzi tego sześcianu? V=a³ a³=64cm³ /³√ a=4cm Sześcian ma 12 krawędzi, więc suma długości krawędzi wynosi 12*4cm=48cm 18. Prawdopodobieństwo zdarzenia A jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do A. Wobec tego prawdopodobieństwo zdarzenia A jest równe: 3P(A)=P(A') wiemy też, że P(A)+P(A')=1 P(A)+3P(A)=1

	1
P(A)=
	4

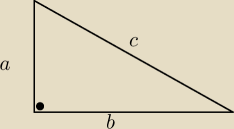
19. Rozwiąż nierówność: x²−42x+441>0 Δ=42²−4*441=1764−1764=0 x²−42x+441=(x−21)² (x−21)²>0 Kwadrat liczby jest nieujemny, więc trzeba wyrzucić iksa kiedy będzie się zerować tj.x=21 x∊R/{21} 20. Przeciwprostokątna trójkąta prostokątnego jest dłuższa od jednej przyprostokątnej o 2cm i od drugiej przyprostokątnej o 9 cm. Oblicz długości boków tego trójkąta. Rysunek do zadania. Z treści wiemy, że b=c−2 oraz a=c−9 a i b są większe od 0, więc c>9 c²=a²+b² c²=(c−9)²+(c−2)² c²=c²−18c+81+c²−4c+4 c²−22c+85=0 Δ=484−340=144 √Δ=12

	22−12
c1=		=5 ∉D
	2

	22+12
c2=		=17 spełnia założenia
	2

c=17, a=8, b=15

Metis: Dla siostry ? Tak to się teraz mówi

Benny: Myślę, że czyta Metis coś sugerujesz?

Metis:

Grzegorz: Cześć ,Mam takie pytanie a nie chce zakladać nowego temu czy 0 na poziomie maturalny zaliczamy do liczb naturalnych? no w zadaniach zamknietych moze z tym być problem bo w otartym zawsze mozna dac komentarz. Dlatego pytam tych co siedzą w temacie

Benny: 21.

	1
Wiedząc, że α jest kątem ostrym i tgα+		=4 oblicz sinα*cosα
	tgα

1		cosα
	=ctgα=
tgα		sinα

	sinα
tgα=
	cosα

	1		sinα		cosα
tgα+		=		+		=
	tgα		cosα		sinα

	sinα		sinα		cosα		cosα
=		*		+		*		=
	cosα		sinα		sinα		cosα

	sin2α		cos2α		sin2α+cos2α		1
=		+		=		=		{cosα}
	sinα*cosα		sinαcosα		sinαcosα		sinα

1
	=4
sinαcosα

	1
sinαcosα=
	4

22. Wykaż, że jeśli a²+b²+2=2a+2b, to a=b=1. a²+b²+2=2a+2b a²+b²+1+1−2a−2b=0 a²−2a+1+b²−2b+1=0 (a−1)²+(b−1)²=0 Suma kwadratów jest zerem, jeśli każdy czynnik jest zerem tj. a−1=0 oraz b−1=0 a=1 i b=1 a=b=1 c.n.w 23. Ciąg (2, x, y−2) jest arytmetyczny, natomiast ciąg (x, y, 16) jest geometryczny. Oblicz x oraz y i podaj ten ciąg geometryczny.

	a1+a3
Z własności ciągu arytmetycznego wiemy, że a2=		, a z własności ciągu
	2

geometrycznego wiemy, że b₂²=b₁*b₃

	y−2+2
Mamy więc, że x=
	2

	y
x=
	2

y=2x oraz y²=16x, ale y=2x, więc (2x)²=16x 4x²=16x /:4 x²−4x=0 x(x−4)=0 x=0 lub x=4 y=0 lub y=8 Dla obu zer wychodzi sprzeczność, więc ciąg geometryczny jest postaci (4, 8, 16) x=4 y=8 24. Punkty A=(−6; 0) i B=(20; 0) są wierzchołkami trójkąta prostokątnego ABC o przeciwprostokątnej AB. Wierzchołek C leży na prostej o równaniu y=x. Oblicz współrzędne punktu C. Punkt C ma zatem współrzędne (x_c, x_c) Aby był to trójkąt prostokątny musi być: |AB|²=|AC|²+|BC|² |AB|=√(20−(−6))²=26 |AC|=√(x_c+6)²+x_c² |BC|=√(x_c−20)²+x_c² 26²=(x_c+6)²+x_c²+(x_c−20)²+x_c² 676=xc²+12x_c+36+2x_c²+x_c²−40x_c+400 4x_c²−28x_c²−240=0 /:4 x_c²−7x_c−60=0 Δ=49+240=289 √Δ=17

	7−17
c1=		=−5
	2

	24
c2=		=12
	2

Punkt C ma współrzędne (−5; −5) lub (12, 12)