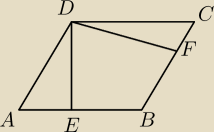
geometria nie: Z wierzchołka D kąta rozwartego równoległoboku ABCD poprowadzono wysokości |DE| i |DF|. Wykaż, że na czworokącie EBFD można opisać okrąg. Oblicz promień tego okręgu, jeśli kąt DAB = 60, |AB| = 8 i |AD| = 6.

g: Kąty BED i BFD są proste, więc ich suma = 180. To wystarczy, żeby móc opisać okrąg. Odcinek BD będzie średnicą tego okręgu, więc R = |BD| / 2. |BD| z twierdzenia kosinusów.

Tadeusz: https://matematykaszkolna.pl/strona/872.html

Mila: 360^o −Suma kątów czworokąta W czworokącie EBFD : |∡E|=|∡F|=90^o zatem ∡B+∡D=180^o Sumy miar kątów przeciwległych mają po 180^o zatem na czworokącie EBFD można opisać okrąg. Środek okręgu opisanego na czworokącie EBFD leży w środku DB. Próbuj dalej sam.