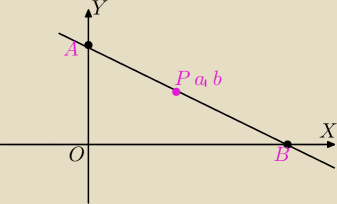
W układzie współrzędnych dany jest punkt P(a,b), gdzie a>0 i b>0. Przez punkt P glax: W układzie współrzędnych dany jest punkt P(a,b), gdzie a>0 i b>0. Przez punkt P poprowadzono prostą, która przecięła dodatnie półosie układu współrzędnych w punktach A i B. Wykaż, że ple trójkąta AOB jest najmniejsze wtedy, gdy punkt P jest środkiem odcinka AB. Oblicz to najmniejsze pole.

glax: up

glax: up

glax: up

glax: up

glax: up

g: Dorysuj jeszcze dwie linie: od punktu P prostopadle do osi X i do osi Y. Powstaną wtedy dwa trójkąty podobne do ABO. Z podobieństwa trójkątów (albo z tangensa jednego z katów) można napisać

A		A−b		Bb		B2b
	=		⇒ A =		⇒ pole = 1/2 AB =
B		a		B−a		2(B−a)

d		B2b		B2b − 2Bab
	(		) =		= 0
dB		2(B−a)		2(B−a)2

⇒ B = 2a, analogicznie A = 2b.

yht: pr. AB: y=mx+n

	n
A(0,n), B(−		,0), P(a,b)
	m

P∊pr. AB → b=m*a+n → n=b−m*a

	OB*OA		−n   *n m		−n2
PΔAOB=		=		=
	2		2		2m

	−(b−m*a)2		−(b2−2b*m*a+m2*a2)
n=b−m*a → PΔAOB =		=		=
	2m		2m

	2b*m*a−b2−m2*a2		b2		m*a2
=		= b*a −		−
	2m		2m		2

	b2		m*a2
P(m) = b*a −		−
	2m		2

	b2		1		a2
P(m) = b*a −		*		−		*m
	2		m		2

	b2		1		a2
P'(m) = 0 −		* (−		) −
	2		m2		2

	b2		a2
P'(m) =		−
	2m2		2

	b2		a2
P'(m) = 0 →		−		= 0
	2m2		2

b2		a2
	=
2m2		2

2a²*m² = 2b² |:2a²

	2b2
m2 =
	2a2

	b2
m2 =
	a2

	b		−b
m=		lub m=		, ale że musi być m<0 oraz a>0,b>0 to
	a		a

	−b
m=
	a

	−b
n=b−m*a = b−(		)*a = b+b = 2b
	a

	−b
prosta AB: y=		x+2b
	a

A=(0,n) = (0,2b)

	−n		−2b
B=(		,0) = (		,0) = (2a,0)
	m		−b   a

Obliczam środek odc. AB: S=(x_S,y_S)

	xA+xB		0+2a
xS=		=		= a
	2		2

	yA+yB		2b+0
yS=		=		= b
	2		2

S=(a,b) Środek odcinka pokrył się z punktem P, zatem P jest środkiem odcinka Obliczam pole:

	OB*OA		2a*2b		4ab
P=		=		=		= 2ab
	2		2		2

glax: Dziękuje g i yht

jc: A może prościej? Podobieństwo trójkątów a : x = (y−b) : y Stąd xy = ay + bx. Nierówność pomiędzy średnią arytmetryczną i geometryczną (ay + bx) /2 ≥ √aybx , równość tylko dla ay=bx czyli xy/2 ≥ √aybx, inaczej xy ≥ 4ab Pole = xy/2 ≥ 2ab jest najmniejsze w przypadku ay = bx, xy = 2ay = 2bx, x=2a, y=2b.