Trapez opisany na okręgu krus: WITAM, czy ktoś dałby rade rozwiązać te zadanie ? http://s5.ifotos.pl/img/aaapng_ssnnhqx.png

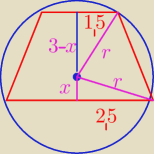
Janek191: Mamy r² = 2,5² + x² = 6,25 + x² r² = ( 3 − x)² + 1,5² = 2,25 +9 − 6 x + x² więc 6,25 + x² = 2,25 + 9 − 6 x + x² 4 = 9 − 6 x 6 x = 5

	5
x =
	6

więc

	5		1		9		25		34
r2 = 6,25 + (		)2 = 6		+ U{25}[36} = 6		+		= 6
	6		4		36		36		36

	250		25*10
r2 =		=
	36		36

	5
r =		√10
	6

============

Werkaa : Hej! Czy umie ktoś rozwiązać ten przykład? Przedstaw wyrażenie w postaci iloczynu: cosα + sin2α − cos3α

glax: sin2α=2sinαcosα cos(α+2α)=cosαcos2α− sinαsin2α=cosα(1−2sin²α)−sinα2sinαcosα= cosα−2sin²αcosα−2sin²αcosα cosα+sin2α−cos3α=cosα+2sinαcosα−cosα+2sin²αcosα+2sin²αcosα=2sinαcosα+4sin²αcosα= 2sinαcosα(1+2sinα)

glax: sin2α(1+2sinα)