plani Jack:

	1
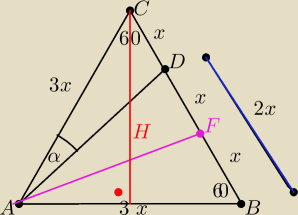
na boku BC trojkata ABC obrano punkt D tak, ze PΔADC =		PΔABC.
	3

oblicz tangens kata CAD, jesli ABC jest rownoboczny. Poprowadzilem prosta AF, tak by bok byl podzielony na 3 rowne czesci. Wydaje mi sie ze kat w takim razie tez bedzie tak podzielony, ale nie umiem tego uzasadnic... i tg 20 stopni to tez nie tak latwo obliczyc

Kacper: Cechy przystawania?

Jack: kbk ? / bkb?

Benny: Wysokość DE łatwo policzyć z pola. Później z trygonometrii bok EC i dalej chyba wiesz jak

Kacper: Lepiej skorzystać z trójkąta 30, 60, 90 stopni

Jack: wysokosc DE latwo policzyc z trojkata 30,60,90. Tak samo bok EC no czyli... niech bok trojkata = 3x DC = x

	x√3
DE (z 30,60,90) =
	2

	x
EC =
	2

zatem

	5x
AE = 3x − x/2 =
	2

	x√3   2		√3
tg alfa =		=		(i to sie zgadza)
	5x   2		5

jednakze , jak bym chcial tym 1wszym sposobem, to jak

Kacper: Te trzy kąty nie są takie same niestety. Dwa z nich tak, ale trzeci już nie

Jack: o o jak to tak mozna

Mila: II

	1		1
|AD|2=a2+(		a)2−2*a*		a*cos(60o)
	3		3

	a√7
|AD|=
	3

	a2√3
PΔACD=
	12

a2√3		1
	=		*|AD|*a*sinα
12		2

a2√3		1		a√7
	=		*		*a*sinα
12		2		3

	√3
sinα=
	2√7

	3
cos2α=1−
	28

	5
cosα=
	2√7

	√3
tgα=
	5

========

Jack: dziekuje wszystkim

Mila:

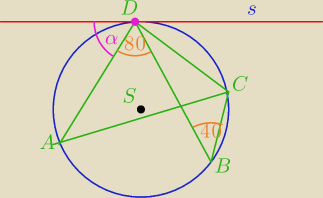
Mila: Zadanie dla Metisa, Jacka s− styczna do okręgu Podaj miarę kąta α.

Metis: α=50 ?

Metis: nie, 60^o ?

Metis: Obie są błędne

ZKS: To zadanie na dobranoc ode mnie. Wielomian W(x)=x²⁰¹³ + ax²⁰¹¹ + bx²⁰⁰⁹ +cx + 6 jest podzielny przez x² + x + 1. Wyznacz resztę z dzielenia wielomianu W(x) przez x² − x + 1.

:): R=12

Metis: Milu α=60^o? Nie chcę podawać rozw. − poczekamy na Jacka

Qulka: 60 na pewno nie

Metis: http://i.imgur.com/BYsLKtL.png

Metis: 2β=2*40 β=40 180−40−80=60

Qulka: 40 to kąt między DC a styczną S więc 60 to α+ten mały kąt BDC

Mila: Problem jest taki. Przyszło do mnie dziecko z takim rysunkiem i stwierdziło, że ma podaną odpowiedź 60^o. To mi nie pasowało ( tak, jak Qulce) . Znalazłam oryginalny zapis treści. Kąt ADC ma miarę 80^o, (łukiem zaznaczono). W podanej treści 22:27 zostawiam do analizy. Trzeba zauważyć, że środek okręgu opisanego na ΔACD leży powyżej AC więc Δ jest ostrokątny.

Metis: Milu czy tym dzieckiem jestem ja ? Nie zbyt rozumiem.

Mila: Nie, to nie o Ciebie chodzi, starszy brat ( uczeń LO , mieszkający blisko mnie) wysłał do mnie młodszą siostrę (gimnazjalistkę) z tym zadaniem. Metis , rozwiąż teraz z poprawioną treścią.

Mila: Porozwiązuj trochę zadań tego typu (najlepiej ze zbioru), zawsze są na maturze.

Metis: Rozumiem Pójdę za radą

Jack: ZKS, ICSP pokazal jak rozwiazac podobne, wiec to chyba banal

Jack: chociaz nie, tamto bylo jednak prostsze ;

ZKS: Jak chcesz możesz zaprezentować rozwiązanie.

Jack: moge jedynie poczatek... W(x) = x²⁰¹³ + ax²⁰¹¹ + bx²⁰⁰⁹ + cx + 6 W(x) = x³(x²⁰¹⁰ −1) + bx²(x²⁰⁰⁷ − 1) +ax(x²⁰¹⁰−1) +x³+bx²+ax+cx+6 wyrazenia w nawiasach sa podzielne... i wlasnie teraz...jakby uzasadnic ta koncowke...hmmm chociaz w tresci napisales ze jest podzielny przez x²+x+1 a ponizej, wyznacz reszte z dzielenia przez x²+x+1 zatem reszta = 0 chyba ze chodzi o wyrazenie reszty poprzez c,a,b

ZKS: Masz wyznaczyć resztę z dzielenia przez x² − x + 1, a nie przez x² + x + 1.

Jack: a widzisz...nie doczytalem : (

Benny: Pierwiastki zespolone i potęgować

Jack: zespolone srednio jeszcze ogarniam, wiec na razie nie chce ryzykowac bledow niestety w liceum ich nie mam

Jack: W(x) = x³(x2010 −1) + bx²(x2007 − 1) +ax(x2010−1) +x³+bx²+ax+cx+6 x³+bx²+ax+cx+6 = x³ + bx² + bx + b + ax + cx + 6 − bx − b = = x³ + b(x²+x+1) + x(a+c−b) + 6 − b dalej nie wymysle ; /

ZKS: Jakie znowu zespolone to zadanie z liceum sam je robiłem w klasie maturalnej.

Jack: kiedys sie robilo trudniejsze zadania w maturalnej

ZKS: Niestety, ja już chodziłem, kiedy były łatwe zadania, nawet mniej było niż teraz, czyli brak pochodnych, granic.

ZKS: Zadanie jest na pomyślenie. Może Metis spróbuje zrobić, jak Ty sobie nie dasz rady.

Metis: Wielomian W(x)=x²⁰¹³ + ax²⁰¹¹ + bx²⁰⁰⁹ +cx + 6 jest podzielny przez x²+x+1. Wyznacz resztę z dzielenia wielomianu W(x) przez x²−x+1. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Wiedząc, że reszta z dzielenia wielomianu W(x) przez trójmian x²+x+1 jest równa 0 , obliczamy resztę z dzielenia W(x) przez x²−x+1 W(x)=(x²+x+1)Q(x)+0 gdzie W(x)=x²⁰¹³ + ax²⁰¹¹ + bx²⁰⁰⁹ +cx + 6 Mamy obliczyć resztę z dzielenia W(x) przez x²−x+1 W(x)=(x²−x+1)P(x)+R

Metis: Zespolonymi naprawdę łatwiej

ZKS: Mogę Ci pokazać, że wcale nie łatwiej.

Metis: Nie pokazuj jeszcze pomyślę

ZKS: Mogę dać wskazówkę, o ile będziecie chcieli.

ZKS: Jasne, jasne nie miałem zamiaru teraz Ci pokazywać, spokojnie pomyśl.

:): R=12 wpis ....... 12 kwietnia 23:26

Jack: ja jak zawsze nie mam czasu na takie bajery... wiadomosc ze (x²−x+1)(x²+x+1) = (x²+1)² − x² nam nic nie daje, co nie : D

ZKS: Raczej nie tędy droga.

:): Wskazówka P(x)=x²+x+1 to P(−x)= x²−x+1

Jack: dobra, to tam, powodzenia Metis. ciekawe jak to wyliczyl ; )

Metis: Mam, ale nie wiem czy to nie bzdura

Benny: : ) na czym Ty jesteś?

Metis: x²⁰¹³ + ax²⁰¹¹ + bx²⁰⁰⁹ +cx + 6= (x²+x+1)Q(x) x²⁰¹³ + ax²⁰¹¹ + bx²⁰⁰⁹ +cx + 6= (x²−x+1)P(x)+R x²⁰¹³ + ax²⁰¹¹ + bx²⁰⁰⁹ +cx + 6= (x²+x+1)Q(x) −x²⁰¹³ − ax²⁰¹¹ − bx²⁰⁰⁹−cx + 6= (x²+x+1)Q(x)+R −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− O to chodzi, czy bzdura?

Metis: Musiałbym sobie to na mniej skomplikowanym przykładzie przeanalizować.

:): i dalej tak : −(x²⁰¹³+ax²⁰⁰¹¹+bx²⁰⁰⁹+cx+6)−12= ............

ZKS: Okej, więc W(x) = (x² + x + 1)Q(x), to teraz W(−x) = ?

ZKS: Eee tam przecież to całe rozwiązanie : ).

ZKS: Tam winno być −(x²⁰¹³ + ax²⁰¹¹+bx²⁰⁰⁹ + cx + 6) + 12 =

Metis: A to co zapisałem to bzdura? :

:): Literówka .... + 12 jak podał ZKS ( dzięki za poprawkę

ZKS: Tylko napisz dalej, bo na razie nie widzę żeby to coś dawało.