Obwód i pole równoległoboku. Matiass: W równoległoboku ABCD krótsza przekątna DB ma długość 20 cm. Wysokość trójkąta ACD poprowadzona z wierzchołka D dzieli odcinek AC na odcinki mające długość 9 i 25 cm. Oblicz obwód i pole tego równoległoboku.

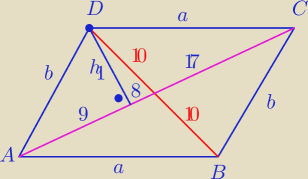
Janek191: Mamy (h₁)² + 8² = 10² ⇒ h₁ = 6 b² = 9² +(h₁)² = 81 + 36 = 117 b = √117= 3√13 ============= a² = (h₁)² + 25² = 36 + 625 = 661 a = √661 ======== Pole P = 2* 0,5 *IAC I*h₁ = 34*6 = 204 [j²] Obwód L = 2 a + 2b = 2*( √661 + 3√13)