przedstaw liczbę w postaci potęgi o podstawie 2
timek:
1.przedstaw liczbę w postaci potęgi o podstawie 2
{64−1/3 * 321/2 * 4−9/2}
______________________
{21/3*256−1/6*8−5/3}
2. Rozwiąż nierówność
a) (2/5)3x−1 > 4(pier 10)/125
b) 1/3 < 3x2−3x+1 ≤ 39−x
3. Naszkicuj wykres funkcji f(x) = 1 −|log2|x−4||. Wyznacz miejsca zerowe tej funkcji i
przedziały,
w których przyjmuje ona wartości nie mniejsze niż −2.
4. Liczba 32log827 jest równa:
A.27 B.128 C.243 D.256
11 kwi 20:23
timek: ktoś pomoże rozwiązać ?
12 kwi 06:22
Jack: 4.
log8 27 = log23 33 = log2 3
32log2 3 = 25log2 3 = 35 = 243
12 kwi 07:02
Jack: 1.64 = 25
Dalej nie widze co tam sie stalo.... Sam spróbuj rozpisac...zamoeniaj na 2 co mozesz
12 kwi 07:06
timek: 1.przedstaw liczbę w postaci potęgi o podstawie 2
{64 −1/3 * 32 1/2 * 4 −9/2}
______________________
{2 1/3 * 256−1/6 * 8 −5/3}
12 kwi 16:51
timek:
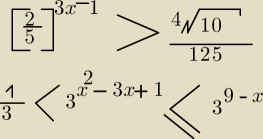
12 kwi 16:56
timek: może ktoś rozwiązać ? 1,2,3
12 kwi 19:41
timek: ma ktoś czas ?
12 kwi 20:53
Qulka:
| 2−2•25/2•2−9 | |
| = 2−5/2 |
| 21/3•2−8/6•2−5 | |
12 kwi 21:02
Qulka: 2. 3x−1=5/2 więc x=35/30
−1<x2−3x+1≤9−x
więc dwie nierówności .. delta ... i część wspólna potem
−1<x2−3x+1 x2−3x+1≤9−x
12 kwi 21:07
Qulka:
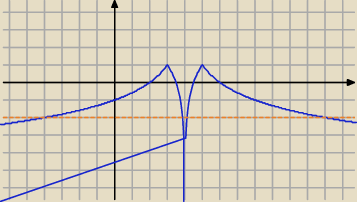
y= 1 −|log2|x−4||.
12 kwi 21:10
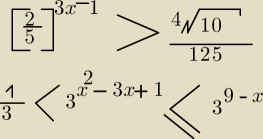
 y= 1 −|log2|x−4||.
y= 1 −|log2|x−4||.