asd Benny: 1.

	25
Liczbę		zaokrąglamy do 3,6. Błąd względny tego przybliżenia jest równy:
	7

	25		18		125−126		1
Δx=|		−		|=|		=
	7		5		35		35

	Δx		1		7		1
δ=		*100%=		*		*100%=		*100%=0,8%
	25   7		35		25		125

2. Liczba 16³*64²=(2⁴)³*(2⁶)²=2¹²*2¹²=2²⁴ 4.

	1
logx		=−4
	9

	1
x−4=
	9

x⁴=9 /⁴√ x=√3 5. Dany jest ciąg (a_n) o wyrazie ogólnym a_n=n²−1, gdzie n≥1. Wówczas a_n+1=? a_n+1=(n+1)²−1=n²+2n+1−1=n²+2n 6.

	7x−1		11
Rozwiązaniem równania		=		jest:
	3x+1		5

3x+1≠0

	−1
x≠
	3

33x+11=35x−5 35x−33x=11+5 2x=16 x=8 7. Liczba pierwiastków rzeczywistych wielomianu W(x)=−3(x²+9)(x−2) jest równa: Tylko dla x=2 wielomian się zeruje, więc jest to jedyny pierwiastek. 8. Mniejsza z dwóch liczb spełniających równanie x²−x₆=0 jest: x²−x−6=(x−3)(x+2) x=3 lub x=−2 Mniejsza z liczb x=−2 9.

	cos70o
Wartość wyrażenia		*tg70o wynosi:
	cos20o

cos20^o=cos(90^o−70^o)=sin70^o

cos70o
	*tg70o=ctg70o*tg70o=1
sin70o

10. Wskaż m dla którego funkcja liniowa określona wzorem f(x)=(m+1)x−3 jest stała: Funkcja liniowa jest stała, jeśli współczynnik przy x jest zerem. m+1=0 ⇔ m=−1 11. W ciągu geometrycznym (a_n) dane są a₁=7 i a₄=−56. Iloraz tego ciągu jest równy: a₄=a₁*q³ −56=7*q³ q³=−8 /³√ q=−2 12. Miara kąta wpisanego opartego na tym samym łuku co kąt środkowy o mierze 52^o jest równa. Wiemy, że miara kąta środkowego jest dwa razy większa od miary kąta wpisanego opartego na tym samym łuku, więc miara kąta wpisanego to 26^o 13. W ciągu arytmetycznym a₁=−6 oraz a₃₀=24. Wtedy suma S₃0 jest równa:

	a1+a30
S30=		*30=(−6+24)*15=270
	2

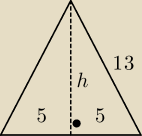
14. Podstawa trójkąta równoramiennego ma długość 10, a ramię ma długość 13. Wysokość opuszczona na podstawę ma długość: Rysunek do zadania. 13²=h²+5² 169−25=h² 144=h² h=12 15. Promień okręgu o równaniu (x+3)²+(y−1)²=25 jest równy: Równanie okręgu jest postaci (x−a)²+(y−b)²=r², więc w tym przypadku r=5.

Benny: 3.

	9−x
Wartość wyrażenia		dla x=9−√3 jest równa:
	x−9

9−x		−(x−9)
	=		=−1
x−9		x−9

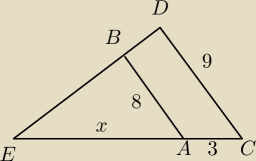
Benny: 16. Oblicz długość odcinka AE wiedząc, że AB||CD, |AB|=8, |AC|=3, |CD|=9 Trójkąty ABE oraz CDE są podobne.

|AB|		|AE|
	=
|CD|		|AE|+|AC|

8		x
	=
9		x+3

9x=8x+24 x=24 17. Objętość walca o promieniu podstawy r i wysokości 2 razy mniejszej od promienia jest równa:

	1
h=		r
	2

V=πr²*h

	1
V=πr2*		r
	2

	1
V=		πr3
	2

18. Graniastosłup ma 18 krawędzi. Ile wierzchołków ma ten graniastosłup? Z każdego wierzchołka wychodzą 3 krawędzie, ale każda krawędź jest liczona dwa razy, więc:

	3
Liczba krawędzi=Liczba wierzchołków *
	2

k−liczba krawędzi w−liczba wierzchołków

	3
k=w*
	2

	2
w=k*
	3

	2
w=18*
	3

w=12 19. Wszystkich liczb dwucyfrowych o różnych cyfrach jest: Liczbę dziesiątek możemy wybrać na 9 sposobów, bo nie może być to zero. Liczba jedności nie może być taka sama jak liczba dziesiątek, ale dodatkowo mamy 0, więc też na 9 sposobów. Liczb dwucyfrowych o różnych cyfrach jest 9*9=81

Metis: Benny , powtarzasz podstawę?

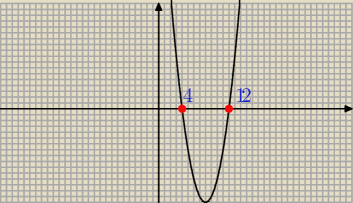
Benny: 20. Rozwiąż nierówność: x²−16x+48≤0 Δ=256−192=64 √Δ=8

	16−8
x1=		=4
	2

	16+8
x2=		=12
	2

(x−4)(x−12)≤0 Rozwiązaniem nierówności są iksy dla których wartości funkcji są niedodatnie. Zachodzi to dla x∊<4;12>

Benny: W sumie to można tak powiedzieć

Metis:

Benny: 21. Rozwiąż równanie x³−2x²−4x+8=0 x³−2x²−4x+8=x²(x−2)−4(x−2)=(x−2)(x²−4)=(x−2)(x−2)(x+2)=(x−2)²(x+2) (x−2)²(x+2)=0 ⇔ x=2 lub x=−2 22.

	b2
Uzasadnij, że jeśli a≠0 oraz		=2b−a2, to b=a2
	a2

b2		2b−a2
	=
a2		1

b²=(2b−a²)a² b²=2a²b−a⁴ b²−2a²b+a⁴=0 (b−a²)²=0 b=a² c.n.w 23.

	5
Kąt α jest ostry oraz tgα=		. Oblicz sinα+cosα
	12

sinα		5
	=
cosα		12

	5
sinα=cosα
	12

sin²α+cos²α=1 sinα=√1−cos²α

	5
√1−cos2α=		cosα /()2
	12

	25
1−cos2α=		cos2α
	144

144−144cos²α=25cos²α 144=169cos²α

	144
cos2α=
	169

	12
cosα=		ponieważ kąt jest ostry
	13

	144		5
sinα=√1−		=		(tamto jest jednym pierwiastkiem)
	169		13

	12		5		17
sinα+cosα=		+		=
	13		13		13

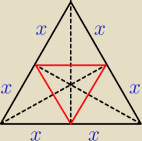
24. Suma n początkowych wyrazów ciągu arytmetycznego (a_n) wyraża się wzorem S_n=2n²+n dla n≥1. Oblicz pierwszy wyraz ciągu i jego różnicę. a_n=S_n−S_n−1 S_n−1=2(n−1)²+n−1 S_n−1=2n²−4n+2+n−1=2n²−3n+1 a_n=2n²+n−2n²+3n−1 a_n=4n−1 a₁=3 r=a_n−a_n−1 a_n−1=4(n−1)−1=4n−5 r=4n−1−4n+5=4 25. W trójkącie równobocznym ABC połączono środki wysokości otrzymując trójkąt KLM. Oblicz stosunek pól trójkątów ABC i KLM.

	1
Otrzymany trójkąt jest równoboczny o długości x=		a, gdzie a to długość boku trójkąta ABC.
	2

k − stosunek długości boków

	a
k=		=2
	1   a 2

k² − stosunek pól k²=4

Eta: Co Ty Benny ..... zdrowy jesteś?

Benny: Jasne, że tak. Nie wiesz, że Nam podstawę na studiach zmienili?