Zadanie optymalizacyjne Parka: Ze wszystkich prostokątów o polu 20, wybierz ten ktory ma najkrótszy obwod. Nie wiem jakie to równanie wymyślić.. Mam na razie a*b=20 F(b)= 2* ²⁰_b + 2b = ⁴⁰_b + 2b Nie wiem czy dobrze myśle, ale z tego ma razie pochodnej nie wylicze...

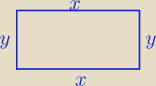
Mila: P=x*y, x>0 i y>0

	20
x*y=20⇔y=
	x

L=2x+2y

	20		40
L(x)=2*x+2*		=2x+
	x		x

	40
L'(x)=2−
	x2

	40		40
L'(x)=0⇔2−		=0⇔2=		⇔2x2=40
	x2		x2

x²=20 x=√20=2√5 L'(x)>0 i x>0⇔x²−20>0⇔x>2√5 dla x=2√5 funkcja L(x) ma wartość najmniejszą.

	20
y=		=2√5
	2√5

odp. najmniejszy obwód ma prostokąt o bokach x=2√5, y=2√5 L=4*2√5=8√5

Rafal44: Inny, mniej szkolny sposób. Obwód danego prostokąta jest największy, kiedy dla a i b będącymi długościami jego boków suma (a+b) jest największa. Dla a i b zachodzi nierówność (a+b)²≥4ab=80, czyli równoważnie (a−b)²≥0, przy czym równość zachodzi wtedy i tylko wtedy, gdy a=b. Wobec tego szukany prostokąt jest kwadratem...

Rafal44: Przepraszam pomyłka, obwód najmniejszy, suma najmniejsza.