wektory szarlotka: każdy z wektorów u i w ma dodatnie wspolrzedne i dlugosc 10. wektor u jest prostopadly do prostej 3x + 4y − 8=0 a wektor w do prostej y = ⁷₂₄ + 4. Wyznacz dlugosc wektora u + w. nie wiem jak to ugryzc

Janek191: Popraw zapis II prostej

szarlotka: y = ⁷₂₄ x +4

Janek191: → u = [ 3a, 4 a ] i √(3a)² + ( 4 a)² = 10 ⇒ √ 25 a² = 10 ⇒ 5a = 10 a = 2 więc → u = [ 6, 8 ] ======== Dokończ To zadanie było już rozwiązywane − szukaj na forum

szarlotka: nie rozumiem jak to a sie pojawilo

Janek191:

	7
cd. y =		x + 4 / * 24
	24

24 y = 7 x + 96 7 x − 24 y + 96 = 0 więc → w = [ 7 b, − 24 b] i √(7b)² + (−24b)² = 10 ⇒ √625 b² = 10 ⇒ 25 b = 10

	10
b =		= 0,4
	25

czyli → w = [ 2,8 ; 9,6 ] oraz → → u + w = [ 6, 8 ] + [ 2,8 ; 9,6 ] = [ 8,8 ; 17,6 ] =================================

Janek191: Wektor prostopadły do prostej 3 x + 4 y − 8 = 0 ma współrzędne [ 3, 4] ale nie ma długości 10 tylko √3² + 4² = 5 więc biorę inny wektor prostopadły do tej prostej [ 3a, 4a ] i szukam takiego a, aby długość tego wektora była równa 10.

Janek191: → Jednak wektor w jest zły, bo nie ma obu współrzędnych dodatnich.

Janek191: Nie było czasem minusa w równaniu II prostej ?

szarlotka: z czego to wynika?

szarlotka: nie

Janek191: Wektor prostopadły do prostej 7 x − 24 y + 96 to [ 7, − 24] Jedna współrzędna jest dodatnia, a druga ujemna.

	7
Może było y = −		x + 4 ?
	24

szarlotka: uu nie minusa nie bylo ale zjadlam slowo rownolegly

Janek191:

Janek191: To dlatego nie wychodziło

Janek191: Zamiast 14.31

	7
y =		x + 4
	24

	7		y
tg α =		=
	24		x

więc → w = [ 24 b, 7 b] i √(24 b)² + (7 b)² = √625 b² = 25 b = 10 więc b = 0,4 → w = [ 9,6 ; 2,8 ] ============ → → u + w = [ 6, 8 ] + [ 9,6 ; 2,8] = [ 15,6 ; 10,8] ===================================

szarlotka: dalej tego nie rozumiem jak mam prosta 5x + 3y −6 = 0 to wektor prostopadly u[5,3] a rownolegly? skad tak?

Janek191:

	y		7
tg α =		=
	x		24

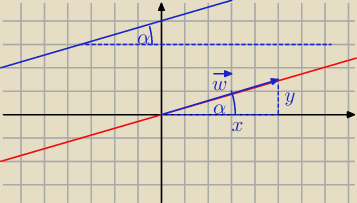
więc y = 7 x = 24 Ale wektor równoległy [ 7, 24 ] ma długość √7² + 24² = √625 = 25 a ma mieć długość 10, więc biorę wektor [ 7b , 24 b ] taki by jego długość była równa 10. Patrz.14.55 → w = [ 9,6 ; 2,8 ] I w I = √ 9,6² + 2,8² = √92,16 + 7,84 = √100 = 10

Janek191: Wyżej powinno być: Ale wektor równoległy [ 24, 7] ma długość √24² + 7² = √625 = 25 a ma mieć 10, więc biorę wektor [ 24 b, 7 b] taki , by ....

szarlotka: w koncu cos mi sie rozjasnilo dzieki

Janek191: Trzeba szukać na forum