matematykaszkolna.pl
planimetria flor:
 |AB| 2 
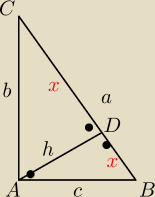
w trójkącie prostokątnym ABC o przyprostokątnych AB i AC mamy
=
. Wysokość
 |BC 5 
 |BD| 
AD dzieli przeciwprostokątną BC na odcinki BD oraz DC. Oblicz
.
 |DC| 
11 kwi 12:45
irena_1: rysunek
c 2 
=
a 5 
 2 
c=
a
 5 
 2 
b2+(
a)2=a2
 5 
 4 21 
b2=a2−
a2=
a2
 25 25 
 √21 
b=
a
 5 
Z pola trójkąta: bc=ah
√21 2 
a*
a=ah
5 5 
 2√21 
h=
a
 25 
x2+h2=c2
 4*21 4 
x2+
a2=
a2
 625 25 
 100−84 16 
x2=
a2=
a2
 625 625 
 4 
x=
a
 25 
 4 21 
y=a−x=a−
a=
a
 25 25 
x 4 
=
y 21 
11 kwi 15:56
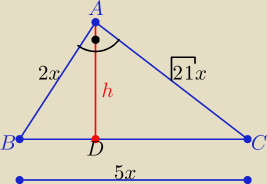
Eta: rysunek
 2x*√21x 2√21 4*21 
x>0 h=
=
x h2=
x2
 5x 5 25 
 212 
|DC|2= 21x2−h2 ⇒ |DC|2=
x2
 25 
h2= |BD|*|DC| / : |DC|2
|BD| h2 |BD| 4*21 25 4 
=
⇒
=
*
=
|DC| |DC|2 |DC| 25 212 21 
11 kwi 16:47
Eta: Przypominam : Obydwa wzory na hc są podane w tablicach wzorów
 ab 
hc=
hc2= |BD|*|DC|
 c 
11 kwi 16:50