styczne do okręgu
Shadow: Wyznacz równania stycznych do okręgu (x−1)2+(y−1)2=4 przechodzących przez punkt P=(−1,−3)
Więc zacząłem od podstawienia do y=ax+b punktu P i obliczyłem b, któro wyszło b=a−3
czyli proste styczne do tego okręgu mają postać y=ax+a−3. Teraz chciałem policzyć wartości a z
odległości między środkiem okręgu a prostą y, jednak po podstawieniu do wzoru wychodzi mi
tylko jedna wartość a, czyli jedna prosta styczna, a przecież ewidentnie są takie proste dwie.
Co zrobiłem nie tak?
10 kwi 22:17
10 kwi 22:19
Janek191:
@ Olekturbo:
Zły wzór
10 kwi 22:21
5-latek : Zawsze się robi do takiego zadania rysunek wtedy widać no chyba z esie jest geniuszsem to nie
potrzeba .
10 kwi 22:21
Janek191:
| | I A x0 + B y0 + C I | |
d = |
| |
| | √A2 + B2 | |
10 kwi 22:22
Janek191:
Ja tu nie widzę geniuszy

Pozdrowienia dla 5 − latka

10 kwi 22:23
Shadow: | | 3 | |
Janek właśnie z tego wzoru skorzystałem, ale wychodzi tylko a= |
| |
| | 4 | |
10 kwi 22:23
Janek191:
Mam zrobić ?
10 kwi 22:24
olekturbo: Cieżko tutaj napisać taki wzór

Moglem dac link do odosnika
10 kwi 22:24
5-latek : Pozdrawiam

10 kwi 22:25
Shadow: Janek jak możesz to możesz zrobić

10 kwi 22:26
5-latek :
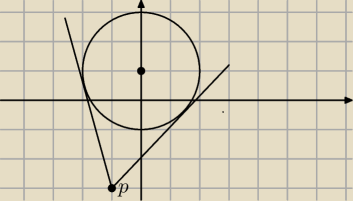
10 kwi 22:27
Janek191:
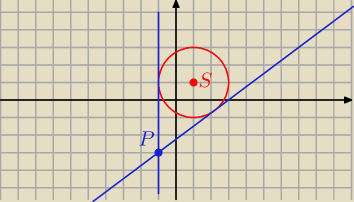
I 2 a − 4 I = 2
√a2 + 1 / : 2
I a − 2 I =
√a2 + 1
a − 2 =
√a2 + 1
=================
Druga styczna ma równanie: x = − 1
10 kwi 22:33
Shadow: właśnie z tą drugą prostą miałem problem, dzięki

10 kwi 22:35
Mila:
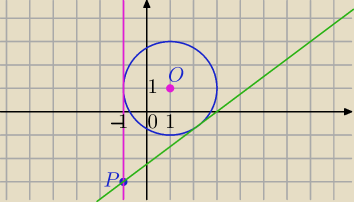
O=(1,1)
Prosta x=−1 nie jest postaci kierunkowej i dlatego nie otrzymałeś korzystając z postaci y=ax+b.
Trzeba tę drugą styczną zauważyć korzystając z wykresu albo:
Trzeba skorzystać z postaci ogólnej równania prostej.
Ax+By+C=0
Spróbuj, jeśli będziesz miał problemy to pisz.
10 kwi 22:47
5-latek : Jak zwykle zaznaczyłem zle srodek okręgu

,

10 kwi 22:59
 Pozdrowienia dla 5 − latka
Pozdrowienia dla 5 − latka
 Moglem dac link do odosnika
Moglem dac link do odosnika



 I 2 a − 4 I = 2√a2 + 1 / : 2
I a − 2 I = √a2 + 1
a − 2 = √a2 + 1
I 2 a − 4 I = 2√a2 + 1 / : 2
I a − 2 I = √a2 + 1
a − 2 = √a2 + 1

 O=(1,1)
Prosta x=−1 nie jest postaci kierunkowej i dlatego nie otrzymałeś korzystając z postaci y=ax+b.
Trzeba tę drugą styczną zauważyć korzystając z wykresu albo:
Trzeba skorzystać z postaci ogólnej równania prostej.
Ax+By+C=0
Spróbuj, jeśli będziesz miał problemy to pisz.
O=(1,1)
Prosta x=−1 nie jest postaci kierunkowej i dlatego nie otrzymałeś korzystając z postaci y=ax+b.
Trzeba tę drugą styczną zauważyć korzystając z wykresu albo:
Trzeba skorzystać z postaci ogólnej równania prostej.
Ax+By+C=0
Spróbuj, jeśli będziesz miał problemy to pisz.
 ,
,