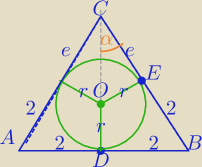
Okrąg wpisany w trójkąt Dawid: W trójkąt równoramienny ABC wpisano okrąg o środku O. Punkt D i E są punktami styczności okręgu oraz odpowiednio podstawy AB i ramienia BC. Oblicz promień okręgu jeśli: |AB|=4, |BC|=2√10

Mila: I sposób |CD|²=(2√10)²−2² |CD|²=40−4=36 |CD|=6

	1
PΔ=		*4*6=12
	2

P_Δ=p*r

	2*2√10+4
p=		=2√10+2
	2

12=(2√10+2)*r 6=(√10+1)*r /*(√10−1) 6*(√10−1)=(10−1)*r

	6*(√10−1)
r=
	9

	2*(√10−1)
r=
	3

========== II sposób |CD|=6 ΔCDB∼ΔOEC⇔

CD		CE
	=		⇔
DB		r

6		2√10−2
	=
2		r

3r=2√10−2

	2(√10−1
r=
	3

===========