proszę pomóżcie Wiksa: Wyznacz rownanie prostej przechodzacej przez punkt (6,1) i równo odległej od punktów A ( 5,−3) i B (−3,0)

5-latek : Potrafisz zrobić tak prosty rysunek do zadania ?

Wiksa: no na kartce umiem narysować to

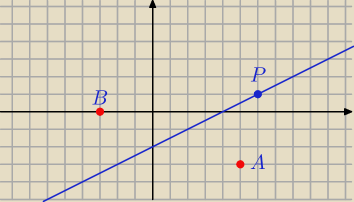
Janek191: Prosta przechodząca przez P =( 6, 1) y = a x + b 1 = 6 a + b ⇒ b = 1 − 6 a y = a x + 1 − 6 a a x − y + 1 − 6 a = 0 A =( 5, − 3) B = ( − 3, 0) więc

I 5 a + 3 + 1 − 6 aI		I − 3 a + 1 − 6 a I
	=
√a2 + 1		√a2 + 1

I 4 − a I = I 1 − 9 a I więc 4 − a = 1 − 9 a lub 4 − a = 9 a − 1 8 a = − 3 lub 5 = 10 a

	−3
a =		lub a = 0,5
	8

wtedy

	18
b = 1 − ( −		) = 3,25 lub b = 1 − 6*0,5 = − 2
	8

	3
y = −		x + 3,25 lub y = 0,5 x − 2
	4

I prosta nie spełnia warunków zadania, Odp. y = 0,5 x − 2 =============

Janek191: ?

Mila: Janku powinna być jeszcze prosta równoległa do AB i przechodząca przez P.

	3
To właśnie ta prosta o wsp. kierunkowym a=−
	8

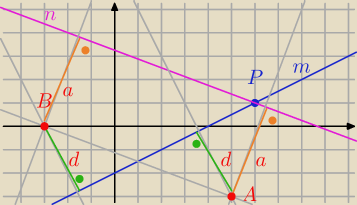Janek191: Dzięki Milu

	3		−3
Napisało mi się −		zamiast		i stąd to nieporozumienie
	4		8

cd.

	3
a = −
	8

	3
y = −		x + b
	8

b = 3,25

	3
n : y = −		x + 3,25
	8

==================

5-latek : A Wiksa ma to w du...e

Janek191: Co prawda, to prawda