jak obliczyć wysokość i krótszą podstawę trapezu Hlna: Trapez równoramienny jest wpisany w okrąg tak, że jego dłuższa podstawa jest średnicą okręgu. Promień okręgu wynosi 5, a ramię trapezu 6. Oblicz wysokość trapezu oraz jego krótszą podstawę.

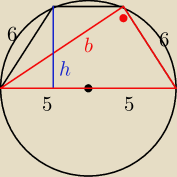
Jack: ja bym policzyl tak: skoro podstawa jest srednica, to trojkat (czerwony) jest prostokatny(z wlanosci ze na srednicy) skoro jest prostokatny to moge obliczyc z pitagorasa trzec bok 10² − 6² = b² b² = 100 − 36 = 64 b = 8

	1
zatem pole tego trojkata mozna obliczyc =		* 6 * 8 = 24
	2

ale pole to mozna obliczyc tez wykorzystujac wysokosc trapezu

	1
czyli to pole =		* h * 10 (2 promienie) = 5h
	2

skoro to pole = 24

	24
5h = 24 −>>> h =
	5

Janek191:

Hlna: A co z krótszą podstawa

Jack: a po co Ci ona

Hlna: bo to wynika z polecenia do zadania

Jack: a, fakt, nie czytalem do konca to sam policz ; D

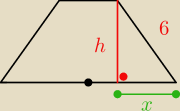
Jack: z pitagorasa oblicz x nastepnie krotsza podstawa = 2R − 2x

Hlna: tak liczyłem, tylko,że wychodzą bzdury, bo x jest równy pierwiastek z 12 i dwudziestu czterech dwudziestu pięciu

Jack: a masz do tego odp. ?

Jack: 6² − h² = x²

	24
62 − (		) = x2
	5

korzystam ze wzoru (a−b)(a+b) = a² − b² zeby bylo latwiej

	24		24
(6 −		)(6 +		) = x2
	5		5

	6		54		324
x2 =		*		=
	5		5		25

	18
x =
	5

dalej Ty

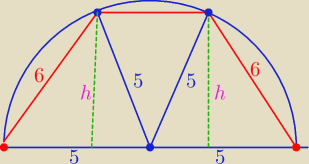
Janek191: Do mojego rysunku: h² + x² = 25 h² + ( 5 − x)² = 36 Odejmujemy stronami ( 5 − x)² − x² = 11 25 − 10 x + x² − x² = 11 10 x = 14 x = 1,4 więc b = 2 x = 2,8 ========= h² = 25 − x² = 25 − 1,4² = 25 − 1,96 = 23,04 h = 4,8 ======

Hlna: nie to zadanie ze sprawdzianu, na którym nie zrobiłem tego zadania, a było ono obowiązkowe na pozytywną ocenę i dlatego byłem ciekawy jak to wyliczyć , bo poległem właśnie na obliczniu podstawy, h mi wyszło tak jak tobie

Eta:

	6*8
h=		= 4,8
	10

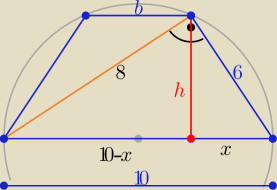
h²=x(10−x) ⇒ 4,8²=x(10−x) 3,6*6,4=x(10−x) ⇒x=3,6 b=10−2x ⇒ b= 2,8