Funkcja f określona na zbiorze liczby rzeczywistych jest funkcją rosnącą.
Zuzia : Funkcja f określona na zbiorze liczby rzeczywistych jest funkcją rosnącą. Wiedząc, że punkty:
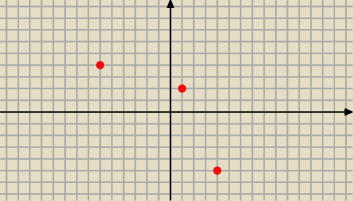
(−6, 4), (1,2) i (4, −5) należą do jego wykresu, wyznacz wartość f(−2√−2 ).
10 kwi 20:07
5-latek : Jeśli mam dane 3 punkty i napisane jest ze te punkty naleza do pewnego wykresu funkcji to już
nie musimy sprawdzać czy te punkty sa współliniowe
Wobec tego żeby okrelic wartość tej funkcji dla argumentu x=−2√−2 (dalej nie pisze gdyż
√−2 nie istnieje w liczbach ℛ
Sprawdz dokładnie tresc zadania
10 kwi 20:38
Janek191:
10 kwi 20:40
Zuzia : Nadal nie rozumiem. Treść zadania została przepisana dobrze.
10 kwi 20:41
Janek191:
10 kwi 20:42
Zuzia : Mój błąd... f(−2√2 )
10 kwi 20:42
Janek191:
Z wykresu widać, że funkcja nie jest rosnąca
10 kwi 20:43
5-latek : To jedno
Druga sprawa jest taka . Masz pierwiastek stopnia drugiego . czy może być pod pierwiastkiem
stopnia parzystego liczba ujemna jeli rozpatrujemy liczby rzeczywiste ?
10 kwi 20:45
Zuzia : Funkcja f określona na zbiorze liczby rzeczywistych jest funkcją nierosnącą. Wiedząc, że
punkty:
(−6, 4), (−3,2), (1,2) i (4, −5) należą do jego wykresu, wyznacz wartość f(−2√2 ).
Przepraszam za błędy, mój chłopak źle mi podyktował
10 kwi 20:48
5-latek : Tresc zadania jest nadal zla
10 kwi 20:52
Janek191:
Te trzy punkty nie określają jednoznacznie wykresu funkcji, więc jak obliczymy f( − 2√2) ?
10 kwi 20:53
Janek191:
Może masz podany wykres tej funkcji ?
10 kwi 20:54
10 kwi 20:55
5-latek :
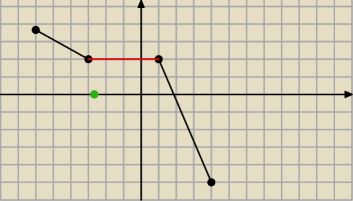
A nie ma być funkcja nierosnaca to dobrze x=−2
√2≈2,82
Potrafisz odczytac z wykresu ?
10 kwi 20:57
Janek191:
Jeżeli wykres tej funkcji składa się z półprostych i odcinków, to
f( − 2√2) = 2
10 kwi 20:58
Zuzia : Odpowiedź do zadania to 2.
10 kwi 21:00
Zuzia : Więć dlaczego 2 i jak to obliczyć ?
10 kwi 21:04
5-latek : Tutaj nie trzeba nic obliczac
Potrzebne sa wiadomości z gimnzazjum (kiedy ja chodziłem do szkoły to mielismy w szkole
podstwowej)
Widzisz na wykresie ze dla x∊<−3,1> funkcja ta jest stala i ma wykres y=2
a nasze x=−2√2 należy do tego przedzialu
Wiec dla jakiegokolwiek x z tego przedzialu wartość funkcji wynosi 2
TO teraz zobaczyny czy to rozumiesz
Ile by wynosila wartość funkcji dla tego argumentu jeśli funkcja bmiala wzor y=4 ?
10 kwi 21:14
Diana: 6
10 kwi 21:16
Diana: −6 *
10 kwi 21:17
5-latek : Nie y=4
10 kwi 21:29
