Wielomiany zef: Wielomian W(x)= (9x²+12x+4)*R(x) jest stopnia czwartego. Podaj przykład wielomianu r(x) takiego aby wielomian w(x) był podzielny przez wielomian P(x)=3x³+5x²+2x Nie jestem pewien czy dobrze myślę nad tym zadaniem. Żeby wielomian w(x) był stopnia czwartego to r(x) musi być stopnia drugiego czyli postać ax²+bx+c I co dalej ? Z p(x) wyłączyłbym jeszcze x przed nawias i policzyłbym miejsca zerowe funkcji kwadratowej która zostanie i zamienił to na postać iloczynową, ale jak to zapisać ?

kochanus_niepospolitus:

	5		2		2
P(x) = 3x3 + 5x2 + 2x = x(3x2+5x+2) = 3x( x2 +		x +		) = 3x(x+1)(x+		)
	3		3		3

Masz już wiedzę, jakie pierwiastki musi (na pewno) posiadać W(x) A teraz sprawdzasz jakie już ma zapewnione:

	2
9x2 + 12x+4 = (3x)2 +2*(3x)*2 + (22) = (3x+2)2 = 9(x+		)2
	3

Więc: R(x) = x*(x+1) (na przykład)

zef: Na skróty tutaj zrobiłeś ale chodzi mi o to jak zapisać to teoretycznie przy pomocy W(x), P(x) i R(x) ?

zef: w(x)=(3x+2)(3x+2)=(x+2/3)(x+2/3) P(x)=x(3x²+5x+2)=x(x+1)(x+2/3) W(x)*R(x)=P(x) (No i tutaj nie wiem czy zapis jest dobry bo teraz bym wyznaczył wielomian r(x) dla którego ten iloczyn byłby równy p(x)) (x+2/3)(x+2/3)*R(x)=x(x+1)(x+2/3) (x+2/3)*R(x)=x(x+1) No i nie wiem co dalej.

zef: Możesz mi to jeszcze jakoś dokładniej wytłumaczyć ? Byłbym bardzo wdzięczny

kochanus_niepospolitus: R(x) = a(x−x₁)(x−x₂) <−−− ogólna postać wielomianu R(x)

zef: No to rozumiem, ale jak wyszedł wynik x(x+1) ?

kochanus_niepospolitus: i nie prawdą jest że W(x) = (9x²+12x+4)*R(x) = P(x) ... P(x) ma DZIELIĆ (bez reszty) W(x), a nie być mu równy

zef: Właśnie wiem, ale jak ja mam to zapisać ?

kochanus_niepospolitus: W(x) = (9x²+12x+4)*R(x) = (9x²+12x+4)*a(x−x₁)(x−x₂) W(x) będzie podzielny przez P(x) = 3x(x+1)(x + 2/3) jeżeli np. R(x) = ....

zef: Czyli 3x²+3x tez może być ?

zef: Wielomian w(x) przy dzieleniu przez dwumiany (x+2), (x−5) daje reszty odpowiednio równe 15 oraz 8. Wyznacz resztę z dzielenia wielomianu w(x) przez p(x)=x³−4x²−7x+10 wiedząc że w(1)=0 Mniej więcej wiem jak się zabrać z takie zadanie, czyli: w(−2)=15 w(5)=8 w(1)=0 w(x)=p(x)*q(x)+r(x) i teraz podstawiam, ale moje pytanie brzmi jak ustalić stopień r(x) ? Bo teraz nie wiem czy zapisać to jako ax²+bx+c czy ax+b a może w ogóle 3 stopień ?

zef: Potrafi ktoś pomóc ?

Mila: W zadaniu z 21:18 ?

zef: Między innymi ale chodzi mi ogólnie. Czy tu chodzi o to że stopień R(x)< st.P(x) ? Czyli jeśli p(x) jest stopnia 3 to r(x) ma być stopnia drugiego ? Dobrze to rozumiem ?

Mila: Jeżeli dzielisz W(x) przez p(x)=x³−4x²−7x+10 to reszta jest stopnia co najwyżej stopnia drugiego. R(x) ma postać : R(x)=ax²+bx+c Tyle pomocy wystarczy?

zef: Tak, przed chwilą właśnie sam się nad tym zastanawiałem i zrozumiałem że ta reszta musi być mniejszego stopnia niż p(x) albo być równa 0 (wtedy wielomiany są równe) Dziękuje za pomoc, z zadaniem już sobie poradzę

zef: mam trójkąt równoramienny o bokach 10 10 16. Mam obliczyć wysokość poprowadzoną do ramienia. obliczyłem H=6 ale jak obliczyć tą wysokość poprowadzoną do ramienia ?

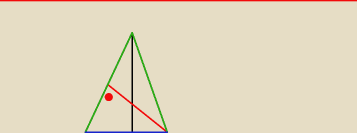
zef: Zielone=10 Niebieskie=16 Czarne=6 Szukane czerwone wie ktoś jak znaleźć ?

Mila:

	1
PΔ=		a*h
	2

h_a=6

	1
PΔ=		*16*6=8*6
	2

	1
PΔ=		*10*hb=5*hb
	2

5*h_b=6*8

	6*8
hb=
	5

zef: No przecież... Jeszcze raz wielkie dzięki.

Mila: