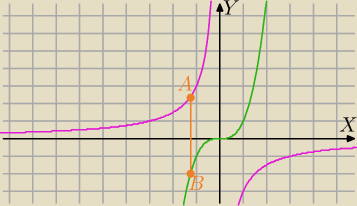
glax glax: Rozpatrujemy odcinki równoległe do osi OY, których jeden koniec leży na wykresie funkcji

	−3
f(x)=		, gdzie x<0,a drugi koniec leży na wykresie funkcji g(x)=x3, gdzie x∊R. Oblicz
	x

długość najkrótszego takiego odcinka.

	−3
punkty mają współrzędne A(x,		) B(x,x3)
	x

	3
wyznaczam sobie funkcję długości tego odcinka h(x)=|x3+		| ∧ x<0
	x

	3
h(x)=−x3−		x<0
	x

	3
h'(x)=−3x2+		x<0
	x2

	3
h'(x)=0 ⇔ −3x2+		=0
	x2

−x⁴+1=0 (x−1)(x+1)(x²+1)=0 x<0 x=−1 f(1)=4 lim_x→0− f(x)=+∞ lim_x→−∞ f(x)=+∞ lim_x→0− f(x)=lim_x→−∞ f(x)=+∞ Jak to zadanie zakończyć? czy funkcja w tym punkcje osiąga wartość największą i najmniejszą?

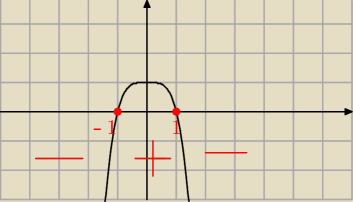
kochanus_niepospolitus: granice zbytecznie policzone wystarczy zrobić szkic wykresu pochodnej h(x) (bez ograniczania się dla x<0) i pokazać, że w x=−1 masz minimum lokalne Największej NIGDY nie przyjmie (wykazałeś to licząc granice). W sumie to wychodzi na to, że liczysz 'coś', ale sam do końca nie wiesz co takiego liczysz.

glax: mi wychodzi, że −1 to maksimum chyba że coś pokręciłem

kochanus_niepospolitus:

glax: kochanus−niepospolitus czy na mój wynik mogło mieć znaczenie, że pomnożyłem równanie przez −1 ?

kochanus_niepospolitus: ale oczywiście NIGDY, PRZENIGDY nie mnoży się (przy patrzeniu na monotoniczność) przez (−1) czy też jakąkolwiek ujemną liczbę przemnożenie przez (−1) nie zmieni 'usytuowania' ekstremum lokalnego ... ale jak sam zauważyłeś ... wywróci 'do góry nogami' monotoniczność funkcji

kochanus_niepospolitus: dlatego ... zawsze przy badaniu monotoniczności 'olewa'(/mnoży) się tylko i wyłącznie te wartości, które są NA PEWNO dodatnie np. Ty olałeś mianownik (x²) w pewnym momencie ... w trakcie tego powinieneś napisać, że: ∀{x∊D_f') x² > 0

glax: kurcze to dlatego mi wyszło, że −1 jest maksimum dzięki kochanus−niepospolitus za pomoc i za uświadomienie tak ważnej rzeczy

kochanus_niepospolitus: m.in. ze względu właśnie na monotoniczność NIGDY/PRZENIGDY nie redukuje się nic w pochodnej typu:

	f
(		)'
	g

ponieważ w takiej pochodnej (bez redukcji) w mianowniku będzie g² ... czyli wyrażenie dodatnie ... czyli możemy 'olać to' przy wyznaczaniu monotoniczności

kochanus_niepospolitus: przykład:

	ln(−x)
f(x) =		(pomijam już zabawy z dziedziną itd.)
	x2

	−x − 2xln(−x)
f'(x) =		<−−− z tej postaci badamy monotoniczność, a nie z:
	x2

	−1−2ln(−x)
f'(x) = ........ =		<−−− z tej (chyba że się przemnoży teraz przez 'x2' czyli
	x

wróci do tego co było wcześniej)

glax: już zrozumiałem o co biga