Dany jest trójkąt ABC w którym |AC|>|BC|. Na bokach AC i BC tego trójkąta obrano odpowiednio
takie punkty D i E że zachodzi równość |CE|=|DE|. Proste AB i DE przecinają się w punkcie F.
Wykaż że kąt BCA= kątowi BAC + AFD
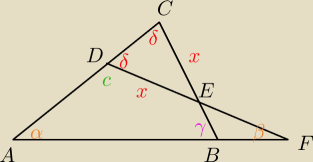tak trudno PODPISAĆ wierzchołki i kąty 
Kąty δ mamy bo ΔCDE jest równoramienny (patrz dane zadania).
c = 180 − δ
c = 180 − α − β ... czyli α+β = δ