help mat: Na bokach AB, BC, CD i DA czworok ˛ata ABCD wybrano punkty K, L, M i N takie, ze˙ AK/KB =BL/LC =CM/MD =DN/NA = k, gdzie k ∈ (0, +∞). Oblicz stosunek pola czworok ˛ata KLMN do pola czworok ˛ata ABCD

kochanus_niepospolitus: skąd przekopiowane zadanie

mat: a czy ma to jakies znaczenie

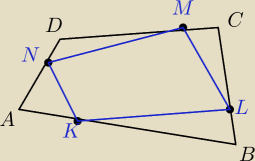
g: Pole czworokąta ABCD można policzyć posługując się współrzędnymi wierzchołków i iloczynem wektorowym: S₁ = (B−A)x(C−B) + (C−B)x(D−C) + (D−C)x(A−D) + (A−D)x(B−A) Punkty K,L,M,N dadzą się wyrazić poprzez A,B,C,D i liczbę k:

	kB+A		kC+B		kD+C		kA+D
K =		L =		M =		N =
	1+k		1+k		1+k		1+k

Pole KLMN liczę tak samo:

	k(C−B)+(B−A)
(L−K) =
	1+k

	[k(C−B)+(B−A)] x [k(D−C)+(C−B)]
(L−K)x(M−L) =
	(1+k)2

	k2(C−B)x(D−C) + k(B−A)x(D−C) + (B−A)x(C−B)
=
	(1+k)2

(zauważ że k(C−B)x(C−B) = 0, więc nie wszedł) Teraz cztery takie iloczyny trzeba zsumować, ale warto najpierw się przyjrzeć ostatniemu wyrażeniu. Składniki typu k²(C−B)x(D−C) zsumują się do k²*S₁. Składniki typu (B−A)x(C−B) zsumują się do S₁. Składniki k(B−A)x(D−C) się poskracają dzięki własności a x b = − b x a.

	k2S1 + S1
S2 =
	(1+k)2

	S2		1+k2
ostatecznie		=
	S1		(1+k)2

mat: Niezbyt rozumiem ten iloczyn wektorowy, jest inny sposób

Mila: Jest.

mat: A jaki

Mila: Dużo pisania. Czekaj, obyś tylko przeczytał później.

mat: No jasne. To zadanie z probnej matury info niby za 4 pkt tylko

Mila:

AK
	=k⇔
KB

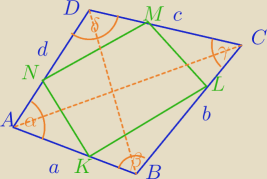
|AK|=k*|KB| i |AK|+KB|=a⇔ k*|KB|+KB|=a |KB|*(k+1)=a

	a		k*a
|KB|=		i |AK|=
	k+1		k+1

Analogicznie obliczysz pozostałe zależności:

	k*b		b
|BL|=		i |LC|=
	k+1		k+1

	k*c		c
|CM|=		i |MD|=
	k+1		k+1

	k*d		d
|DN|=		i |NA|=
	k+1		k+1

Liczymy sumę pól naroży: ( zaczynam od wierzchołka A)

	1		d		k*a		a		k*b
Sn=		*(		*		*sin α +		*		*sinβ+
	2		k+1		k+1		k+1		k+1

	b		k*c		c		k*d
+		*		*sinγ+		*		*sinδ)=
	k+1		k+1		k+1		k+1

	k		1		1		1		1
=		*(		*ad*sinα+		*ab*sinβ+		*bc*sinγ+		*cd*sinδ)=
	(k+1)2		2		2		2		2

	k
=		*(PΔBAD+PΔABC+PΔBCD+PΔADC)=
	(k+1)2

	k
=		*2PABCD
	(k+1)2

	k		2k
PKLMN=PABCD−		*2PABCD=PABCD*(1−		)
	(k+1)2		(k+1)2

PKLMN		2k   PABCD*(1− )   (k+1)2
	=		=
PABCD		PABCD

	2k		k2+1
=(1−		)=
	(k+1)2		(k+1)2

==========================

Mila: O gdybym wiedziała, że z info to nie pisałabym. Nie możemy tego robić.