styczne do wykresu funkcji glax: Dana jest funkcja f(x)=x³−3x²+2x+3, określona w zbiorze liczb rzeczywistych. Wyznacz miary kątów α nachylenia do osi OX wszystkich stycznych do wykresu funkcji. Funkcja f(x) jest różniczkowalna f(x)=x³−3x²+2x+3, x∊R f'(x)=3x²−6x+2, x∊R i co dalej wiadomo, że tgα=a=f'(x_o)

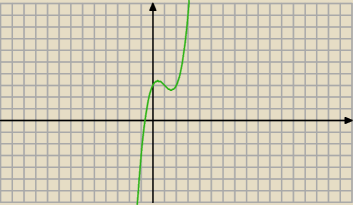
Jerzy: Jest ich nieskończenie wiele

glax: Odp:.α∊<0,90^◯) ∪ <135^◯,180^◯) jak do tego dojść?

Benny: f'(x)=3x²−6x+2 Zwf=3(x²−2x+1)−1=3(x−1)²−1 Zwf=<−1;+∞) Teraz badaj kiedy tangens przyjmuje takie wartości.

glax: jak do rozwiązania dojść? tgα=−1⇔ α=135^o tgα=0 ⇔ α=0^o v tgα=180^o tgα=1 ⇔ α=45^o tg90^o nie istnieje

glax:

glax:

glax: ktoś zerknie na to zadanie?

glax:

ZKS: Gdzie jest problem?

glax: w dokończeniu tego zadania

ZKS: Kąt nachylenia prostej w jakim przedziale się zawiera?

glax: Wyznacz miary kątów α nachylenia do osi OX wszystkich stycznych do wykresu funkcji.

ZKS: Zadałem pytanie Tobie.

glax: (0^o,180^o)

ZKS: Dlaczego wyrzuciłeś 0 oraz 180^o? Teraz masz rozwiązać nierówność tg(x) ≥ −1 dla x ∊ [0 ; π].

Metis: Cześć ZKS Mam jedno pytanie z analizy Pomożesz?

ZKS: Hej Metis. Jeżeli będę w stanie pomóc to oczywiście.

glax: x∊<O^o, 90^o)∪<135^o,180^o>

ZKS: glax i co było takie trudne?

glax: w odpowiedziach jest wyrzucone jeszcze 180^o. ZKS z twoją pomocą było łatwiej dziękuje

ZKS: Tego Ci nie powiem może traktują 0 oraz 180^o jako to samo, że prosta nie zmienia położenia względem osi OX.

glax: dziękuje jeszcze raz ZKS

ZKS: Nie ma za co, proszę bardzo.

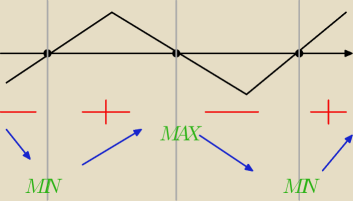
Metis: Badam monotoniczność funkcji . Moje f'(x)= 2(x+3)(x²−5)=0 Rysuję przybliżony wykres pochodnej: I teraz nie wiem czy dobrze nazywam: Funkcja f(x) ma 3 ekstrema : 2 minima lokalne , jedno maksimum lokalne( które jest jednocześnie maks. globalnym ) . I teraz muszę zbadać, które z minimum jest minimum globalnym czyli najmniejszą wartością funkcji , tak?

Jerzy: Minimum globalne to najmniejsza wartość funkcji w całej dziedzinie ( podobnie maksimum)

Metis: Czyli jest ?

ZKS: Minimum (maksimum) globalne funkcji to jest to samo, co wartość najmniejsza (największa) funkcji, zatem maksimum globalne u Ciebie nie będzie tylko lokalne, ponieważ maksimum globalne wynosi ∞. Za to minimum globalne będziesz miał.

Jerzy: maksimum globalne wynosi ∞ ?

Jerzy: funkcja nie osiąga wartości największej, a więc nie ma max globalnego

ZKS: Napisałem tak, aby Metis zrozumiał dokładnie o co chodzi.

Jerzy: A tak patrząc na pochodną ..... jaka jest najmniejsza wartosć tej funkcji, jeśli dziedziną jest R ?

Metis: To ta funkcja: http://www.wolframalpha.com/input/?i=0.5x%5E4++%2B+2x%5E3+-+5x%5E2+-+30x+-+1 Wolfram pokazuje, że jest maksimum i minimum lokalne. Nie wiem jak nazwać to co otrzymałem, bo z badania wychodzi, że minima są dwa: w x=−3 i x=√5

Jerzy: przecież dla x < − 3 funkcja stale maleje , więc jak ma minimum globalne ?

ZKS: Metis czytaj uważnie. Napisane tam jest Local maximum oraz Global minimum.

Metis:

Metis: ZKS jasne... nie wiem jak to czytałem

Jerzy: OK ... minimum globalne dla x = √5 i brak maksimum globalnego

Metis: Wątpliwości rozwiane Dzięki

ZKS: Maksimum masz tylko lokalne, natomiast minimum masz dwa lokalne z czego jeden jest minimum globalnym.

Metis: Dokładnie