asd olekturbo: w(x) = x³−x²−2x+1 ile pierwiastków ma ten wielomian w przedziale (−2;2) ? w'(x) = 3x²−2x−2 I co teraz

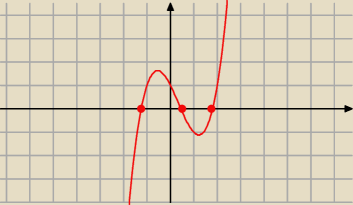
jc: W(−2) = −7 W(0) = 1 W(1) = −1 W(2) = 1 W każdym z przedziałów : (−2,0), (0,1), (1,2) mamy zatem co najmniej jeden pierwiastek, w sumie co najmniej 3. Wielomian 3 stopnia nie może mieć więcej niż 3 pierwiastki. Dlatego w przedziale (−2,2) mamy dokładnie 3 pierwiastki.

Janek191: w '(x) = 0 ⇔ 3 x² − 2 x − 2 = 0 Δ = 4 − 4*3*(−2) = 4 + 24 = 28 = 4*7 √Δ = 2√7

	2 − 2√7		1		1		1		1
x1 =		=		−		√7 x2 =		+		√7
	6		3		3		3		3

x₁, x₂ ∊ ( − 2, 2) więc mamy dwa ekstrema f(− 2) = − 8 − 4 + 4 + 1 = − 7 f(0) = 1 f(1) = − 1 f(2) = 1 więc funkcja ma 3 miejsca zerowe w ( − 2, 2).

Janusz: Zbadaj znak w'(x) i przedziały monotoniczności wielomianu w(x). Odp: jedno miejsce zerowe.

olekturbo: dzieki