oj
ojojojoj:
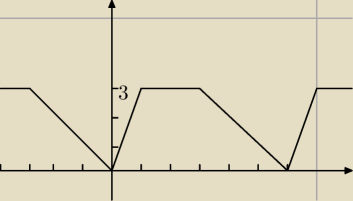
f(x)=
| | ⎧ | 3x−18k, jeśli x∊<6k,1+6k> | |
| | ⎨ | 3, jeśli x∊<1+6k,3+6k>, gdzie k∊ℤ |
|
| | ⎩ | −x+6+6k, jeśli x∊<3+6k,6k+6k> | |
Zbadaj, czy istnieje pochodna funkcji f w punktach: 8,2015,−2015. Jeśli tak to wyznacz jej
wartość.
9 kwi 12:51
ojojojoj: up

9 kwi 12:59
ojojojoj: ...
9 kwi 13:26
ojojojoj: up
9 kwi 13:52
ICSP: Gdzie jest problem ?

9 kwi 13:53
ojojojoj: | | ⎧ | 3, jeśli x∊<6k,1+6k> | |
| f'(x)= | ⎨ | 0, jeśli x∊<1+6k,3+6k>, gdzie k∊ℤ |
|
| | ⎩ | −1jeśli x∊<3+6k,6k+6k> | |
co dalej?
9 kwi 14:08
ICSP: Zacznij od ciągłości.
9 kwi 14:13
ojojojoj: jak sprawdzić czy jest ciągła

9 kwi 14:26
ojojojoj: granice liczyć...
9 kwi 14:31
ICSP: Granica jednostronne muszą być równe wartości funkcji w punkcie.
9 kwi 14:36
ojojojoj: nie umiem tego policzyć

9 kwi 14:42
ICSP: Dobra. Załóżmy, że jest ciągła. Znajdź teraz reszty z dzielenia przez 6 liczb :
8
2015
−2015
9 kwi 14:44
ojojojoj: 8=6+2
2015=2010+5
−2015=−2010−5
9 kwi 14:45
ICSP: 8 = 6 * 1 + 2 , k = 1, 8 wpada w środek drugiego przedziału, a w całym drugim przedziale
funkcja jest ciągła i rózniczkowalana jako funkcja stała, więc w szczególności w punkcie x = 8
ta funkcja jest różniczkowalana.
Pozostałe robisz identycznie.
9 kwi 14:47
 f(x)=
f(x)=



