prawdopodobieństwo geometryczne klasyk: 2.Losujemy dwa punkty A i B z odcinka [0,1]. a)Jaka jest szansa, że środek odcinka AB będzie należał do przedziału [0,1/3]? b)Jakie jest p−stwo, że A ma bliżej do B niż do 0? a) moc Ω = <0,1> * <0,1>

	1
A − środek odc AB należy do <0;		>
	3

	a+b		1
A = {(a,b) należy do Ω:		≤		}
	2		3

	2
Wychodzi nam z tego trójkąt równoramienny o bokach długości		.
	3

Nie wiem co zrobić z tym zrobić dalej b)

	3
P(B) =		− ( 1/2*1/2 dla przypadku a<b ; i 1/2 dla przypadku a>b )
	4

Mógłbym prosić o dokładniejszy opis podpunktu b, bo nie bardzo rozumiem dlaczego tak jest. Z góry dziekuję za pomoc

zzz: Również podłączam się do pytania

g:

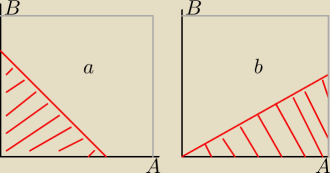
	A+B
a)		≤ 1/3 ⇒ A+B ≤ 2/3 ⇒ P = (2/3)2 / 2 = 2/9
	2

b) A > B/2 ⇒ P = 1 − 1/4 = 3/4

jc: (b) prawdopodobieństwo, że a<b jest takie samo, jak prawdopodobienstwo, że a>b, zatem każde z tych prawdopodobieńst wynosi wynosi 1/2. Jeśli b < a, to na pewno a jest bliżej b niż liczby 0. Przy założeniu, że 0<a<b, prawdopodobieństwo, że a znajdzie się bliżej 0 jest takie samo jak prawdopodobieństwo, że znajdzie się bliżej b. Dlatego prawdopodobieństow to wynosi 1/2. Szukane prawdopodobieśtow = 1/2 + 1/2*1/2 = 3/4