Geometria analityczna Zuza: Okrąg O1 o środku w punkcie (4, −2) jest styczny do osi OX. Okrąg ten przekształcono przez

	3
jednokładność o skali k= −		i środku w punkcie P należącym do prostej x + 2y = 0. W ten
	2

sposób otrzymano okrąg O2. Podaj równanie okręgu O2, jeśli jest on styczny do osi OY.

5-latek : Co do tej pory oprocz napisania zadania zrobilas ?

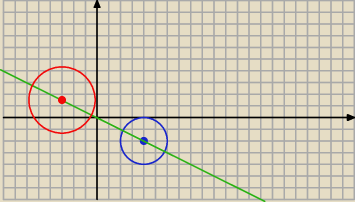
Janek191: S₁ = ( 4, − 2) r₁ = 2 r₂ = I k I * 2 = 3 więc S₂ = ( − 3, 1,5) bo y = −0,5*(−3) = 1,5 Odp. ( x + 3)² + ( y − 1,5) = 9 ======================

Janek191: Odp. ( x + 3)² + ( y − 1,5)² = 9

Zuza: Obliczyłam promień drugiego okręgu r=3, choć nie mam pewności czy jest to dobrze i wyznaczyłam punkt styczności pierwszego okręgu z osią OX i wiem, że r1=2

Zuza: Już wszystko rozumiem, dziękuję bardzo

Janek191: