wartość bezwzględna w równaniu nikitka96: Wyznacz wszystkie wartości parametru a , dla których równianie ||x+2|−3|=a−x ma nieskonczenie wiele rozwiązań Zakoduj pierwsze trzy cyfry rozwinięcia dziesiętnego ilorazu iloczynu znalezionych wartości przez ich sumę. W odpowiedzi zakodowano 125. Nie wiem dlaczego... Na forum znalazłam takie rozwiązanie: Niezależnie od przedziału, na którym rozpatrujemy badane równanie, ma ono postać (1) sx + b = a − x, gdzie s = −1 lub s = 1. Jest to więc równanie liniowe. Równanie takie ma nieskończenie wiele rozwiązań tylko wtedy, gdy s = −1 i b = a. Jak łatwo zauważyć współczynnik s przy x w wyrażeniu ||x+2| − 3| jest ujemny, gdy 1° x+2 ≥ 0 i jednocześnie x+2−3 < 0, wtedy −2 ≤ x < −1, zaś występujący w (1) współczynnik b jest równy +1 albo 2° x+2 < 0 i jednocześnie −x−2−3 ≥ 0, wtedy x ≤ −5, zaś współczynnik b jest równy −5. Odpowiedź: Równanie ma nieskończenie wiele rozwiązań, gdy a = 1 lub a = −5. Sprawdzenie. Dla a = 1 równanie ma postać ||x+2| − 3| = 1 − x, ma ono nieskończenie wiele rozwiązań dla x∊[−2, −1), gdyż na tym przedziale przyjmuje postać |x − 1| = 1 − x, czyli −x + 1 = 1 − x. Dla a = −5 równanie ma postać ||x+2| − 3| = −5 − x, ma ono nieskończenie wiele rozwiązań dla x∊(−∞, 5], gdyż na tym przedziale przyjmuje postać |−x−2−3| = − 5 − x, czyli |x+5| = −5 − x, to znaczy − x − 5 = − 5 − x. ale dalej nie wiem dlaczego zakodowano 125.

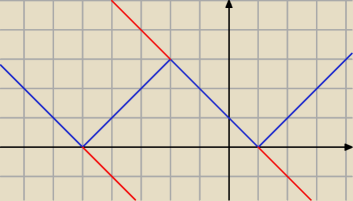
g: Niebieskie to wykres funkcji f(x) = ||x+2|−3| Ta funkcja pokrywa się w nieskończonej liczbie punktów z funkcjami 1−x, oraz −5−x. −5/1 / (1−5) = 1.25

nikitka96: A dlaczego −5−x się pokrywa? jeśli x=0 to czemu wykres nie przecina y=−5?

nikitka96: Przepraszam.... już rozumiem DZIĘKI