 Najpierw kilka równań:
1) c2 = (x*2/3)2 + (y*2/3)2 (środkowe przecinają się 2:1)
2) x2 = a2 +(b/2)2 − 2 ab/2 cos γ
3) y2 = b2 +(a/2)2 − 2 ab/2 cos γ
4) c2 = a2 + b2 − 2ab cos γ
Z sumy 2)+3) wyznaczam −2ab cos γ i wstawiam do 4).
Z 1) wyznaczam x2+y2 i też wstawiam do 4).
Po tych zabiegach wyjdzie równanie na c w funkcji a i b.
Najpierw kilka równań:
1) c2 = (x*2/3)2 + (y*2/3)2 (środkowe przecinają się 2:1)
2) x2 = a2 +(b/2)2 − 2 ab/2 cos γ
3) y2 = b2 +(a/2)2 − 2 ab/2 cos γ
4) c2 = a2 + b2 − 2ab cos γ
Z sumy 2)+3) wyznaczam −2ab cos γ i wstawiam do 4).
Z 1) wyznaczam x2+y2 i też wstawiam do 4).
Po tych zabiegach wyjdzie równanie na c w funkcji a i b.
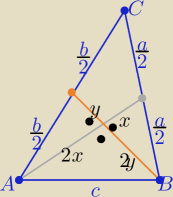 "krótka piłka"
"krótka piłka"  Środkowe w trójkącie dzielą się w stosunku 2:1 licząc od wierzchołka
dodatkowo z treści zadania są prostopadłe
to teraz należy poprosić p. Pitagorasa
Środkowe w trójkącie dzielą się w stosunku 2:1 licząc od wierzchołka
dodatkowo z treści zadania są prostopadłe
to teraz należy poprosić p. Pitagorasa
| b2 | ||
4x2+y2= | ||
| 4 |
| a2 | ||
4y2+x2= | ||
| 4 |
| a2+b2 | c2 | |||
5x2+5y2= | i 4x2+4y2=c2 ⇒x2+y2= | |||
| 4 | 4 |
| a2+b2 | ||
zatem 5c2=a2+b2 ⇒ c=√ | ||
| 5 |

 piszesz ten fakt( w każdym zadaniu) bez uzasadnienia
Czy tw. Pitagorasa też będziesz uzasadniać ?
piszesz ten fakt( w każdym zadaniu) bez uzasadnienia
Czy tw. Pitagorasa też będziesz uzasadniać ?
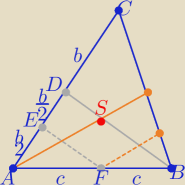 i Tales ...........
i Tales ...........
 czyli nie trzeba ;x
czyli nie trzeba ;x