geometria, dowód
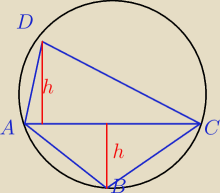
rafal: Czworokąt ABCD jest wpisany w okrąg oraz pola trójkątów ABC i ADC są równe. Wykaż, że:
|AB|2 + |BC|2 + |CD|2 + |DA|2 = 2|AC|2
9 kwi 10:48
Kacper:
biorę

9 kwi 11:13
g:
|AB|
2 + |BC|
2 = |AC|
2 + |AB|*|AC|*cosβ
|CD|
2 + |DA|
2 = |AC|
2 + |CD|*|DA|*cosδ (δ = 180 − β)
Sumuję te dwa równania.
|AB|
2 + |BC|
2 + |CD|
2 + |DA|
2 = 2|AC|
2 + (|AB|*|AC| − |CD|*|DA|)*cosβ
Żeby wyszło to co jest do udowodnienia to musiało by być:
1) β=90 (nie ma takiego wymogu w zadaniu)
2) |AB|*|AC| = |CD|*|DA| (to nie jest prawda).
Wniosek: teza jest nieprawdziwa.
9 kwi 11:34

 |AB|2 + |BC|2 = |AC|2 + |AB|*|AC|*cosβ
|CD|2 + |DA|2 = |AC|2 + |CD|*|DA|*cosδ (δ = 180 − β)
Sumuję te dwa równania.
|AB|2 + |BC|2 + |CD|2 + |DA|2 = 2|AC|2 + (|AB|*|AC| − |CD|*|DA|)*cosβ
Żeby wyszło to co jest do udowodnienia to musiało by być:
1) β=90 (nie ma takiego wymogu w zadaniu)
2) |AB|*|AC| = |CD|*|DA| (to nie jest prawda).
Wniosek: teza jest nieprawdziwa.
|AB|2 + |BC|2 = |AC|2 + |AB|*|AC|*cosβ
|CD|2 + |DA|2 = |AC|2 + |CD|*|DA|*cosδ (δ = 180 − β)
Sumuję te dwa równania.
|AB|2 + |BC|2 + |CD|2 + |DA|2 = 2|AC|2 + (|AB|*|AC| − |CD|*|DA|)*cosβ
Żeby wyszło to co jest do udowodnienia to musiało by być:
1) β=90 (nie ma takiego wymogu w zadaniu)
2) |AB|*|AC| = |CD|*|DA| (to nie jest prawda).
Wniosek: teza jest nieprawdziwa.