Postać Jordana, wektory dołączone Przemysław: czy nie tak właśnie szuka się wektorów dołączonych do wektora v, że rozwiązuje się: (A−x 1|)w=v i w to nasz wektor dołączony, x − wartość własna, 1| − jedynka macierzowa? 5 0 −1 −4 A= 6 1 −3 −5 1 −1 −2 −1 5 0 −1 −4 Chciałbym policzyć postać Jordana macierzy A wartość własna jedna, czterokrotna − 0 dwa wektory własne lin. niezal., np: 1 4 9 1 5 i 0 0 5 jak poszukam wektorów dołączonych to nie istnieją, bo: dla jednego wektora dostanę układ: 5x−z−4w=1 6x+y−3z−5w=9 x−y−2z−w=5 5x−z−4w=0 co jest sprzeczne, bo 1≠0 a dla drugiego 5x−z−4w=4 6x+y−3z−5w=1 x−y−2z−w=0 5x−z−4w=5 co też jest sprzeczne, bo 4≠5 Gdzie się pomyliłem? Bo wiem, że klatki powinny być dwie i jedna rozmiaru 3, jedna rozmiaru jeden.

Przemysław: Błąd w macierzy − powinno być: 5 0 −1 −4 6 1 −3 −5 1 1 −2 −1 5 0 −1 −4

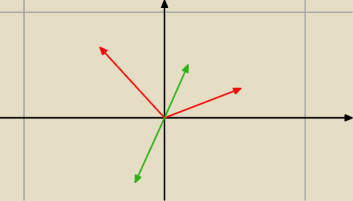
b.: Problem jest w metodzie, tak można szukać wektorów dołączonych, gdy jest jeden wektor własny. Tutaj trzeba znaleźć taki wektor w (dołączony), aby Aw ∊ lin{v₁,v₂}, gdzie v₁,v₂ −− znalezione wektory własne. Rysunek poglądowy: czerwone to v₁, v₂, rozpinają dwuwymiarową podprzestrzeń wektorów własnych, ale tylko wektory v o takim kierunku jak te zielone mają wektory dołączone.

Przemysław: Czyli wiemy, że Aw ∊ lin{v1,v2} i mamy znaleźć w? Ale w to będzie wektor dołączony do którego wektora własnego?

Przemysław: "ale tylko wektory v o takim kierunku jak te zielone mają wektory dołączone." czyli istnieje wyszczególniony wektor własny, wielokrotności którego posiadają wektory dołączone? Czyli wektor dołączony jest tylko dla jakiegoś wektora dającego się uzyskać z kombinacji liniowej bazy podprzestrzeni wektorów własnych? Czyli jakoś trzeba Aw=α*v₁+β*v₂

Przemysław: "wielokrotności którego posiadają wektory dołączone?" Chyba nawet nie wielokrotności, ale dokładnie tylko on.

Przemysław: Tak czy inaczej dziękuję Jakby co to jest jeszcze metoda z jądrami odpowiednich potęg (A−x1|) , więc na razie chyba jej będę używał

b.: no jeśli on, to i wielokrotności zgadza się, tak właśnie będzie. Zauważ, że to, że v ma wektor dołączony oznacza (w przypadku zerowych wart. wł.), że v ∊ Im(A) (gdzie Im jest obrazem odwzorowania) Gdyby jakieś niezależne lin. wektory własne z₁, z₂ miały wektory dołączone, to z_j ∊ Im(A) skąd lin{z₁, z₂} ⊂ Im(A) i w przypadku z zadania (tj. dwywym. przestrzeni wekt. wł.) każdy wektor wł. miałby wektor dołączony. Wtedy można by akurat liczyć tak jak chciałeś na początku. Byłyby 2 klatki po 2. jeśli chodzi o rachunki, to piszemy tak jak o 10:43, czyli mamy układ równań z niewiadomymi w (4 niewiadome skalarne) oraz α,β

Przemysław: α i β chyba muszą być ≠0 No to powiedzmy − rozwiązuje taki układ i dostaję dwa równania ograniczające, czyli wymiar 2, czyli są jakieś dwa wektory dołączone u i w. i teraz to nie jest tak, że powinno zachodzić Au=w A²u=v v − wektor własny? Albo raczej Au=w' gdzie w' też byłoby dobrym wektorem dołączonym? W jakiej kolejności wypisujemy te wektory w bazie Jordana?

b.: te dwa wektory dołączone u i w będą się różniły o wektor własny z wart. wł. 0, więc trzeba któryś z nich wziąć (obojętnie), a potem dalej dołączony do dołączonego

Przemysław: A! Dobra, dziękuję bardzo

Mariusz: "Problem jest w metodzie, tak można szukać wektorów dołączonych, gdy jest jeden wektor własny." Jeżeli jest więcej niż jeden liniowo niezależny wektor własny to chyba można wziąć do szukania wektorów dołączonych taką kombinację liniową tych wektorów tak aby r(A−λI)=r(A−λI | v) gdzie r(A) rząd macierzy A