Prosba 5-latek : Milu Pomoz mi proszse jeszce w cwiczeniach nr 40,41 i 42 strona 64 i na tym zakoncze wielomiany dziekuje

5-latek : Moze napiszse cw nr 40 Od czego zalezy znak wielomianu '' w plus nieskonczonosci'' dla argumentow wiekszych od najwiekszsego jego pierwiastka Kiedy pierwiastki sa rozwiazaniami nierownoci Moze jakis przyklad do tego cwiczenia i nastepnych ?

5-latek : Wiem z e to nie miejsce na tlumaczenie teorii ale zrob wyjatek

5-latek : Cwiczenie nr 41 Czy wielomian zawsze zmienia znak przy przejściu argumentu przez pierwiastek ? Podaj przykład wielomianu W(x) i takiego jesgo pierwiastka x₁ ze W(x)≤0 dla wszystkich x z pewnego przedzialu o srodku x₁ czyli dla x∊(x₁−δ,x₁+δ) gdzie δ jest pewna liczba dodatnia Cwiczenie nr 42. czy wielomian może zmieniac znak w punkcie x₀ nie bedacyn jego pierwiastkiem Jeśli tak podaj i wskaz czynnik zmieniający w x₀ znak w wielomianie rozlozonym na czynniki Jeśli dzisiaj będzie miała czas to prosze zebys mi pomogla w tym

5-latek : Chociaz prosiłem Mile to mysle z esie nie pogniewa jeśli ktoś da cenne dla mnie rady

Jerzy: Cześć 40) zależy od znaku przy najwyższej potędze x 41) nie zmienia, jeśli pierwiastek jest parzysto − wielokrotny 42) nie może

5-latek : Czesc A możesz pokazac na przykładach zebym to zrozumial ?

===: https://matematykaszkolna.pl/strona/142.html

Jerzy: 41) W(x) = (x−2)²*(x−4)³ .... w x = 2 nie zmiania, w x = 4 tak

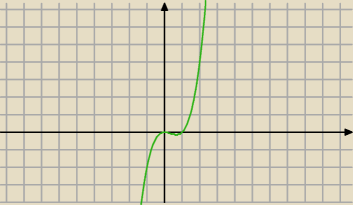
Jerzy: Tutaj masz przykład: W(x) = x²(x −1) ... w x = 0 nie zmienia znaku

5-latek : To znam oczywiście Cw 40 wytłumaczysz ?

===: przecież to oczywista oczywistość

Jerzy: f(x) = W(x) = axⁿ + bxⁿ⁻¹ + .... lim_x→+∞f(x) = +∞ ( gdy a > 0 ) = − ∞ ( gdy a < 0 )

Jerzy: popatrz: f(x) = ax³ + x² + x + 1

	1		1
limf(x) = lim[ax3(1 +		+		)] = ax3*1 = ax3 i znak zależy od znaku a
	x		x3

Jerzy: tam w nawiasie zgubiłem a w mianownikach, ale to bez znaczenia

5-latek : === Pewnie jak rozwiazuje jakies równanie wielomianowe to pewnie z tego nieświadomie korzystam

===:

5-latek : Dobrze J To już kapuje . Teraz bys pokazal na przykładzie cw 42 .

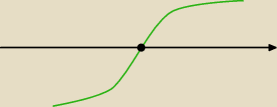
Jerzy: Tuatj trzeba " na zdrowy rozum" ( na studiach to się już dowodzi − tw.Darboux) jeśli dostatecznie bliskim otoczeniu punktu x₀ wielomian zmienia znak, to musi po drodze ( w punkcie x₀) przyjąć wartość 0 , więc jest jego pierwiastkiem

5-latek : To druga liceum i nie było granic i pochodnych

Jerzy: pochodnych nie stosujemy a zamiast granicy, przyjmujemy bez dowodu,że znak zależy od znaku a

5-latek : Na razie dziekuje CI

5-latek : Może Milu cos dodasz od siebie ?

Mila: Jutro dam przykłady. Dzisiaj nie mogłam być wcześniej na forum.

5-latek : Dobrze . Ja dzisiaj tez dopiero niedawno wrocilem od brata

5-latek :

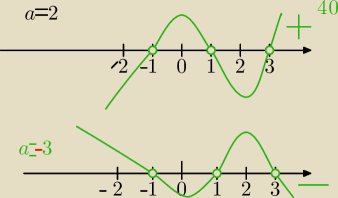
Mila: W zasadzie Jerzy wszystko pięknie wyjaśnił. 40) w(x)=a*(x−1)*(x+1)(x−3) Największy pierwiastek to x=3 2*(x−1)*(x+1)(x−3)>0 −3*(x−1)*(x+1)(x−3)>0 Pierwiastki są rozwiązaniami nierówności ze znakiem : ≥ lub ≤

5-latek : Dziekuje to cwiczenie nr 40 Teraz cwiczenie nr 41 Wiem ze parzystokrptne odbija sie i nieparzyste przechodzi Podaj przykład .itd. (możesz podac ?

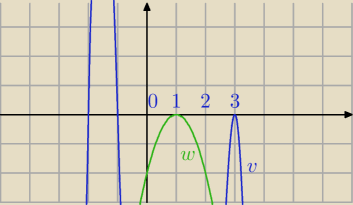
Mila: 41) w(x)=−2(x−1)² najprostszy przykład przy przejsciu przez x=1 wielomian w(x) nie zmienia znaku v(x)=−2*(x−3)²*(x+1)*(x+2) np. v(x)≤0 dla każdego x∊(3−1,3+1) v(x) zmienia znak przy przejściu przez x=−1, x=−2

5-latek : dziekuje CI bardzo Przepraszam ze tak długo nie odpisywałem ale pomagam koleżance Diana . Nie wiem jak ona napiszse mature

5-latek : Jeszcze bardzo Cie proszę to cwiczenie nr 42 . Chyba zajme się tylko swoimi problemami bo tak wychodzi jakbym Cie lekcewazyl a tak nie jest .

5-latek :

Mila: Zmienia znak tylko przy przejściu przez pierwiastek, o ile pierwiastek nie jest parzystej krotności. Nie wiem co autor miał na myśli .

5-latek : No i na tym zakomczmy te wielomiany Proste zadania ,równania i nierownosci potrafie rozwiazywac . Mysle ze to wystarczy . Jeszcze sobie tylko może jutro wyprowadze wzory Vieta dla wielomianu stopnia trzeciego i starczy . Teraz się wezme za funkcje wymierne . Dziekuje za pomoc