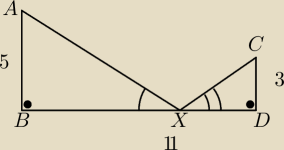
Trójkąty prostokątne złyibrzydki: Punkty A,B,C,D położone są jak na rysunku. Zakładamy, że AB⊥BD, CD⊥BD oraz |AB|=5, |CD|=3,|BD|=11. Niech punkt X należy do odcinka BD. Wykaż, ze suma |AX|+|XC| jest namniejsza wtedy i tylko wtedy, gdy |∡BXA|=|∡DXC| Bardzo proszę o pomoc.

g: Oznaczam: a = |AB|, b = |CD|, c = |BD|, x = |BX|. |AX|+|XC| = f(x) = √a²+x² + √b²+(c−x)² Łatwo można sprawdzić, że jeśli kąty przy X są równe, czyli x/a = (c−x)/b, to pochodna df(x)/dx=0. Można również sprawdzić, że dla takiego x druga pochodna d²f(x)/dx² > 0, czyli że to jest minimum lokalne. Więcej roboty będzie z wykazaniem, że to jest jedyne minimum.