trygo Jack: wyznacz wartosci parametru w, dla ktorych rownanie 2 sinx − 1 = a ma dokladnie 2 rozwiazania w przedziale <0;2π>

Jack: 2 sinx − 1 = w * reszta git

Jack: Czy oto chodzi? 2 sinx − 1 ∊ (−3;1) 2 sinx − 1 > − 3 /\ 2sinx − 1 < 1

Mila: No i co za problem?

Janek191: 2 sin x = w + 1 sin x = 0,5*( w + 1) więc − 1 ≤ 0,5( w + 1) ≤ 1

5-latek : A jaki jest zwaiazek miedzy w i a ?

Jerzy: I gdzie problem ?...2sinx = w + 1

Benny: @Janek191 myślę, że trzeba wyrzucić −1, 0, 1.

Jerzy: Chyba się zdrzemnąłem..

Jack: 5−latku "w" i "a" sa obok siebie na klawiaturze, mialo byc "w" , weszlo "a" tak jak Janek napisal 2sinx = w+1

	w+1
sinx =
	2

	w+1
−1 ≤		≤ 1
	2

jednakze, 2 rozwiazania ma w przedziale obustronnie otwartym, wiec stad

w+1
	> −1 −>>> w+1 > −2 −>>> w > −3
2

	w+1
i		< 1 −>> w+1 < 2 −>>> w < 1
	2

w ∊ (−3;1) jednakze w odpowiedzi jeszcze jest jeden a nie dobra, bo wykluczyli −1 i 1 zatem odp. w ∊ (−3;−1) U (−1;1) dobra, dzieki wszystkim za pomoc

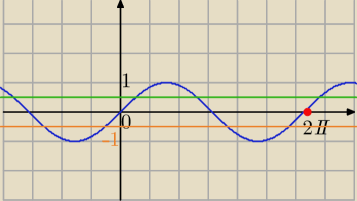
Mila: 2sinx−1=w ⇔ 2sinx=w+1 /:2

	w+1
sinx=
	2

	w+1
0<		<1 /*2
	2

0<w+1<2 /−1 −1<w<1 lub

	w+1
−1<		<0 /*2
	2

−2<w+1<0 /−1 −3<w<−1

Jack: Benny 0 nie zostalo wyrzucone...

Jack: Dzięki Milu

Jerzy: Trafna uwaga Benny

Benny: Jack czemu 0 nie zostało wyrzucone? W takim przedziale sinx=0 ma 3 rozwiązania.

Jerzy: Nie było wpisu

Benny:

Janek191: Dla w = 0

	π		π
mamy 2 sin x = 1 ⇒ sin x = 0,5 ⇔ x =		lub x = π −
	6		6

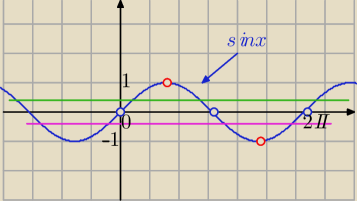
Mila: Zielona linia

	w+1
0<		<1
	2

lub różowa linia:

	w+1
−1<		<0
	2

Benny: Janek191 mi nie chodziło o w=0