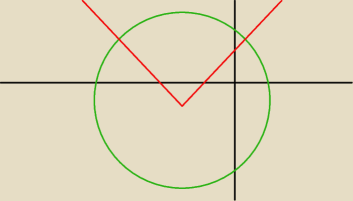
Geometria analityczna Nemesis: Zaznacz w układzie współrzędnych zbiory A i B jeśli: A = {(x, y) ∊ R² : (x+3)² + (y+1)² ≤ 25}, B = {(x, y) ∊ R² : y ≥ |x + 3| − 1} Wyznacz współrzędne środka i promień okręgu wpisanego w wycinek koła będącego częścią wspólną zbiorów A i B. Narysowałem te zbiory ale nie wiem jak mam zacząć wyznaczać ten okrąg wpisany w wycinek. Jakieś wskazówki?

Nemesis:

wmboczek: spróbuj znaleźć pkt równoodległy o ramion kąta leżący na osi symetrii możesz też rozwiązać zadanie z planimetrii R=(1+√2)r

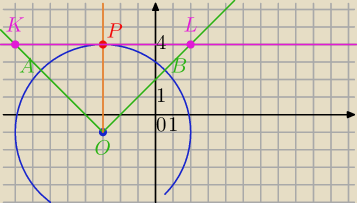
Mila: Środek okręgu wpisanego w wycinek leży na dwusiecznej kąta AOB. Czyli na prostej x=−3 P=(−3,4) − punkt wspólny dwusiecznej i okręgu. Rysujemy styczną do okręgu w p. P Okrąg wpisany w ΔKOL będzie spełniał warunki zadania. Teraz próbuj dokończyć.

Nemesis: Obliczyłem r z pola i szukam punktu równoodległego od boków leżącego na dwusiecznej kąta KOB ale nic nie wychodzi

Nemesis: KOL*

Nemesis: ?

Mila: Jaki masz promień?

Nemesis: 5(√2 − 1)

Mila: Dobrze . S=(−3, 4−r) korzystamy z tego , że Δ jest równo ramienny i S leży na prostej x=−3, |PS|=r

Nemesis: Czemu w S jest 4−r nie powinno być 5−r?

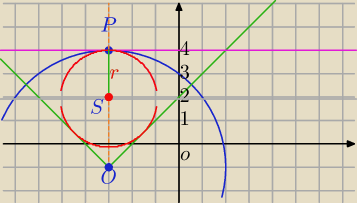
Mila: S=(−3,9−5√2) Od wsp. y=4 punktu P odejmujesz długość promienia.

Nemesis: Okej wszystko jasne. Dziękuje bardzo za pomoc.

Mila:

wiesia: Narysuj dwa okregi(zaznacz ich srodek oraz promien i punkt wspolny)a) niemajace punktu wspolnego b)styczne zewnetrznie c)styczne wewnetrznie d) majace dwa punkty wspulne.narysowac ukladem wspolrzednym