| 4 | 4 | |||
Punkt P(0, −2) jest środkiem podstawy trójkąta równoramiennego, a punkt S( | , − | ) | ||
| 3 | 3 |
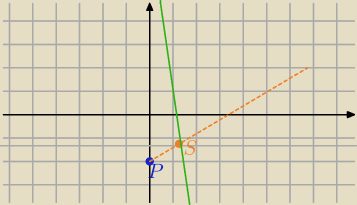 Środkowe Δ przecinają w jednym punkcie i dzielą w stosunku 2:1 licząc od wierzchołka.
|PS|=a
|SC|=2a
Najlepiej wyznacz wektorowo.
SC⊥AB, bo Δ jest równoramienny
Dalej sam?
Środkowe Δ przecinają w jednym punkcie i dzielą w stosunku 2:1 licząc od wierzchołka.
|PS|=a
|SC|=2a
Najlepiej wyznacz wektorowo.
SC⊥AB, bo Δ jest równoramienny
Dalej sam?

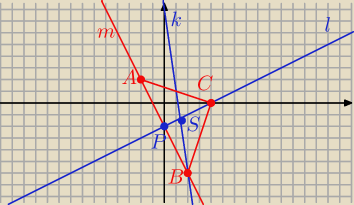
| 4 | 4 | |||
P = ( 0, − 2) S = ( | , − | ) | ||
| 3 | 3 |
| −43 + 2 | ||
y = | x + b = 0,5 x + b | |
| 43 |
| x + 2 | y − 6 | ||
= 0 i | = − 2 | ||
| 2 | 2 |
| 4 | 2 | |||
PS = [ | , | ] | ||
| 3 | 3 |
| 8 | 4 | |||
2 PS = [ | , | ] | ||
| 3 | 3 |
| 4 | 4 | 8 | 4 | |||||
C = S + 2 PS = ( | , − | ) + [ | , | ] = ( 4, 0 ) | ||||
| 3 | 3 | 3 | 3 |