odleglosc punktow od funkcji.
m4rk1: Podany jest punkt A(−5,6) oraz B(−1,4). Wyznacz punkt na funkcji liniowej y = −y − 3 którego
odległość do punktu A i B będzie taka sama.
Proszę o rozwiązanie a nie podpowiedzi. Rozwiązaliśmy to zadanie z kolegami ale wyszły nam
sporne wyniki.
Ja zrobiłem to w taki sposób, że wyznaczyłem prostą przechodzącą przez A i B, wyznaczyłem
środek odcinka AB i stworzyłem prostą prostopadłą do tej funkcji przechodzącą przez ten
środek.
Wyszło mi mniej więcej (7/5, i kurczę y nie pamiętam). To jest zadanie maturalne.
8 kwi 15:52
m4rk1: nikt?
8 kwi 17:26
Mila:
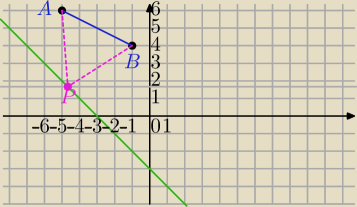
A(−5,6) oraz B(−1,4)
y=−x−3
?
P(x,−x−3), |AP|=|BP|
√(x+5)2+(−x−3−6)2=
√(x+1)2+(−x−3−4)2⇔
(x+5)
2+(−x−9)
2=(x+1)
2+(−x−7)
2⇔
(x+5)
2+(x+9)
2=(x+1)
2+(x+7)
2⇔
x
2+10x+25+x
2+18x+81=x
2+2x+1+x
2+14x+49
28x+106=16x+50
12x=−56
Spr.
| | 14 | | 5 | | 1 | | 13 | | 1+169 | | 170 | |
|AP|2=(− |
| +5)2+( |
| −6)2= ( |
| )2+(− |
| )2= |
| = |
| |
| | 3 | | 3 | | 3 | | 3 | | 9 | | 9 | |
| | 14 | | 5 | | 11 | | 7 | | 121+49 | | 170 | |
|BP|2=(− |
| +1)2+( |
| −4)2=(− |
| )2+(− |
| )2= |
| = |
| |
| | 3 | | 3 | | 3 | | 3 | | 9 | | 9 | |
|AP|=|BP|
8 kwi 18:12
Maciej: A(−5, 6), B(−1, 4), C(x, −x − 3)
d =
√(x2 − x1)2 + (y2 − y1)2
|AC| = |BC|
√(x + 5)2 + (−x − 3 − 6)2 =
√(x + 1)2 + (−x − 3 − 4)2
|AC| = |BC| / ()
2
(x + 5)
2 + (−x − 9)
2 = (x + 1)
2 + (−x − 7)
2
x
2 + 10x + 25 + x
2 + 18x + 81 = x
2 + 2x + 1 + x
2 + 14x + 49
28x + 106 = 16x + 50
12x = −56
8 kwi 18:17