W trójkąt prostokątny o przeciwprostokątnej równej 6 cm justynka: W trójkąt prostokątny o przeciwprostokątnej równej 6 cm i kącie ostrym 30° wpisano okrąg o promieniu a cm. Ile wynosi a? Proszę o rozwiązanie, a nie tylko wynik.

m4rk1: podpowiedz: wykorzystaj wysokości trójkąta.

justynka: Niestety nie wiem co dalej. Próbowałam wymyślić coś z podobieństwa trójkątów ale dalej nic

g:

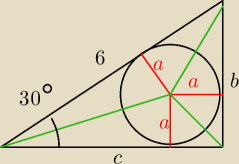
	b*c		6*a + b*a + c*a
Pole trójkąta:		=
	2		2

b = 6*sin 30 = 3 c = 6*cos 30 = 3√3

	b*c
a =		= .... itd.
	6+3+3√3

justynka: Skąd wziąłeś to ^a*b _6+3+3√3

justynka: Może ktoś mi wytłumaczyć?

justynka: ?

g: Z sumy 6*a + b*a + c*a wyciągnij a przed nawias i wyznacz a z tego równania. Następnie wstaw za a i b liczby.

Eta:

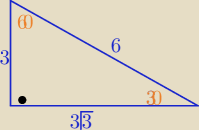
	a+b−c
Ze wzoru w tablicach : r=
	2

	3+3√3−6
r=		= 1,5(√3−1)
	2

skoro w tym zadaniu przez a −− oznaczono dł. promienia r to r=a=1,5(√3−1) [j]