planimetria xxxy:

	2
W trojkacie prostokatnym ABC o przyprostokatnych AB i AC mamy AB: AC =		.
	5

Wysokosc AD dzieli przeciwprostokatna ABC na odcinki BD oraz DC. Oblicz BD : DC.

Przemysław: oznaczmy: x − stała dodatnia, rzeczywista |AB|:=5x |AC|:=2x wtedy: |CB|=x*√29

	1
PΔABC=		*5x*2x=5x2
	2

|AD|=:h − oznaczenie długości ΔABC

1
	*h*x*√29=5x2
2

	10x
h=
	√29

	100x2		16		√29
|CD|=√(2x)2−h2=√4x2−		=x √		=4x
	29		29		29

|BD|=x*√29−|CD|

|BD|		√29   √29−4*   29
	=		=29−4=25
|DC|		√29   29

Bogdan:

h		y		2
	=		⇒ h =		y
2k		5k		5

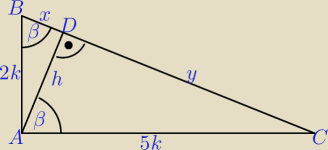
h		y		4		4		x
	=		⇒ h2 = xy ⇒		y2 = xy ⇒		=
x		h		25		25		y

Przemysław: No tak, zgubiłem 4 w mianowniku w ostatniej linijce. Powinno być tam:

	√29		√29
4*		a nie
	29		29

przepraszam za błąd

Zbyszko: Hej Przemek, zgubiłeś i dodatkowo zamuliłeś rozwlekłym zapisem rozwiązanie zadania, takie nieprzejrzyste zapisy rozwiązań odstraszają i utrwalają pogląd o tym, że szkolna matematyka jest nieciekawa i trudna

Przemysław: @Zbyszko Kolejny błąd: 8. linia powinno być "wysokości opuszczonej na BD" zamiast "długości" Przepraszam. Jedyną pociechą jest to, że rozwiązanie jest b. proste w idei, bo z poważniejszych rzeczy korzystam tylko z twierdzenia Pitagorasa i jednego wzoru na pole trójkąta. Sądzę jednak, że nie powinienem był się wypowiadać − istnieje ryzyko wprowadzenia autora tematu w błąd, za co również przepraszam. Jeżeli autor czyta tę wypowiedź, to niech zauważy, że może być dla niego korzystnym jeżeli zignoruje wszystkie moje poprzednie wypowiedzi w tym temacie. Ograniczę umieszczanie potencjalnych rozwiązań do tych, które uznam za faktycznie dobre. Dziękuję za wytknięcie mi błędu − myślę, że można przypuszczać, że Twoja uwaga przyczyni się do poprawy stanu forum, chroniąc je od przynajmniej części tych moich wpisów, które są potencjalnie lub realnie szkodliwe.

xxxy: W kazdym razie wszystkim dziekuje za poswiecenie czasu nad rozwiazaniem