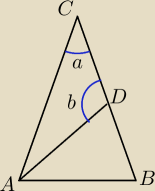
Stereometria Krzycho: Punkt D nalezy do boku BC trojkata rownoramiennego ABC, w ktorym |AC|=|BC|.odcien AD dzieli trijkat ABC na dwa trójkąty rownoramienne w taki sposob ze |AD|=|CD| oraz |AB|=|BD|. Udowodnij ze |<ADC|=5*|<ACD|

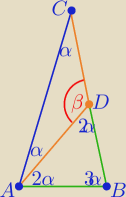
g: Kąty <CAB i <ABC są równe: α + (180−β) = 180 − 2*(180−β) Suma kątów trójkąta ADC: 2α + β = 180 Z tych dwóch równań można wyznaczyć, że β = 5α. Można też wyznaczyć α i β z osobna.

E: 7α=180^o i 2α+β=180^o ⇒ 7α=2α+β⇒ β=5α