pytanie mat: mam funkcję √5x⁴+3x⁴ i mam wyliczyć jej ekstrema Liczę jej pochodną i by w mianowniku nie było 0 to x=0 i x=−3, czy to oznacza, że pochodna funkcji w tym punkcie nie istnieje ?

mat: up

Janek191: Czy dobrze jest przepisane ?

mat: żle masz rację powinno być √x⁵+3x⁴

Janek191: f(x) = √x⁵ +3 x⁴ x⁵ + 3 x⁴ > 0 ⇔ x > − 3 więc

	5 x4 + 12 x3		x3*( 5 x + 12)
f '(x) =		=		= 0 ⇔ x =
	2 √x5 + 3 x4		2√ x5 +3 x4

−2,4

mat: a dla x=0 co z tym

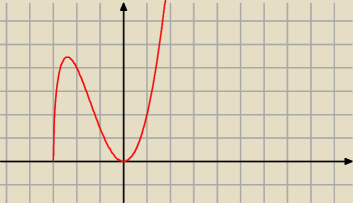
mat: bo mam konkretnie zadanie by obliczyć maks i min funkcji w przedziale (−5,2>

mat: i wychodzi że to min funkcji jest właśnie dla 0

Janek191: W x = 0 jest minimum lokalne równe 0.

mat: ale pochodna w tym punkcie nie istnieje tak Czyli może być ekstremum mimo że nie ma w tym punkcie pochodnej

Janek191: f(x) ≥ 0 dla x ∊ ( − 3 , + ∞) oraz f(0) = 0, więc w zerze jest minimum lokalne.

Janek191: Z definicji minimum , a nie z twierdzenia.

mat: ale pochodna w tym nie istnieje, dobrze myślę

Janek191: Tak.

mat: No bo jak patrzę to w definicji chyba jest że jak jest ekstremum to pochodna tej funkcji ma wartość 0. A Tu pochodna nie istnieje więc o co chodzi?

Janek191: Czy funkcja f(x) = I x I ma w x_o = 0 minimum ? A co z pochodną ?

mat: ok chyba kumam, czyli nie jest wymagana pochodna by było ekstremum, jednynie zmiana znaku pochodnej.

Janek191: Def. Funkcja f określona w otoczeniu punktu x₀ ma w punkcie x₀ maksimum lokalne, jeżeli istnieje taki przedział Δ = ( x₀ − δ , x₀ + δ) , że f(x) ≤ f(x₀) , dla x ∊ Δ.